The National Institute for Mathematical Sciences (NIMS) presents a very special NIMS-IMAGINARY exhibition in collaboration with the ICM committee and the Mathematisches Forschungsinstitut Oberwolfach (MFO). It will feature the best of all IMAGINARY modules of the last years and a lot of new software, images, films and sculptures. It will be the biggest IMAGINARY exhibition shown so far.
FroZenLight
programme
[|||Desktop|||] Double click on the jar file or right click on it and select open with jre/jdk/java. Select museum from the menu for a touchscreen view. Or start it with java -jar frozenlight-1.2.2.jar -f -mu from the command line to get a touchscreen.If you are upgrading from version 1.1.1 delete the .frozenlight folder in your home directory before starting the 1.2.x version.
[|||Android|||] Go to Configuration->Security and allow installation from unknown sources. Tap on the frozenlight-0.1.1.apk file in your file manager to install the app.
Site internet
Contributeurs
A project byZoltan Palmer
Événements associés
The Heidelberg Laureate Forum Foundation invites you to visit the exhibition “Mathematics of Planet Earth” at Karlstorbahnhof in Heidelberg, Germany! It runs from July 5 to Aug 2, 2015, for the first time in Heidelberg. It offers a big variety of exciting adventures for children and adults alike.
Des miroirs de forme circulaire disposés selon une grille réfléchissent les rayons de lumière en fonction des lois de l’optique géométrique. Alors qu’une position aléatoire de la source de lumière produit des structures de réflexion chaotiques, il est possible de positionner la source de lumière de sorte que de belles structures symétriques de réflexion apparaissent.
Cette application vous permet de changer de manière interactive les paramètres tels que la position de la source de lumière, le rayon des cercles ainsi que l’angle de rotation du réseau. Grâce à un menu simple, il est possible de sélectionner et d’explorer un large pan de structures symétriques de réflexion.
Galerie d'utilisateur sélectionnée
All images in this gallery are made with the open source software FroZenLight available at http://frozenlight. altervista.org
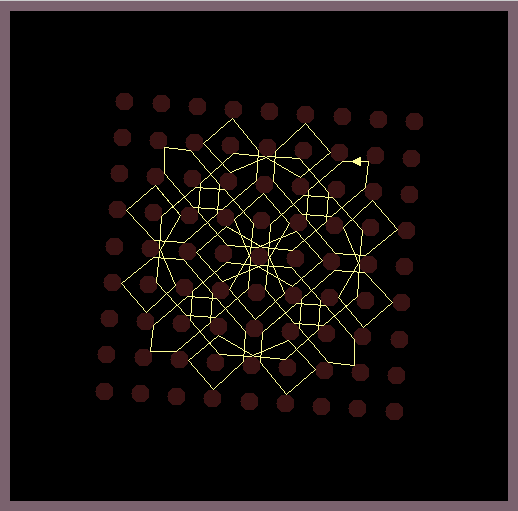
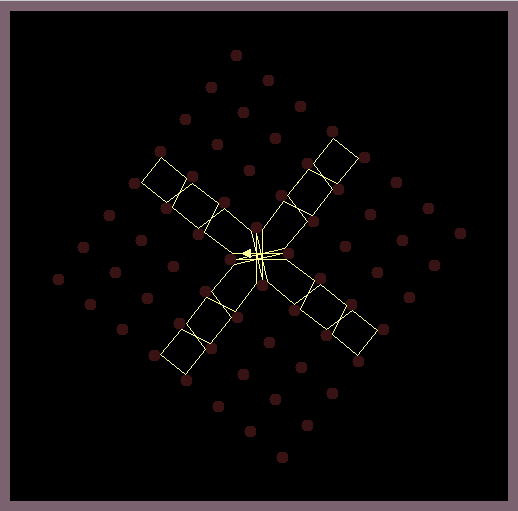
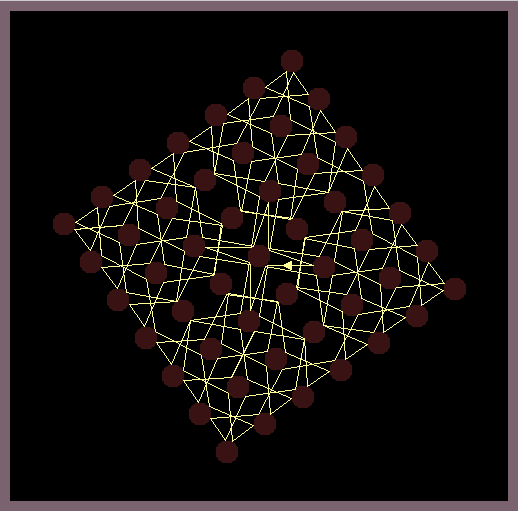
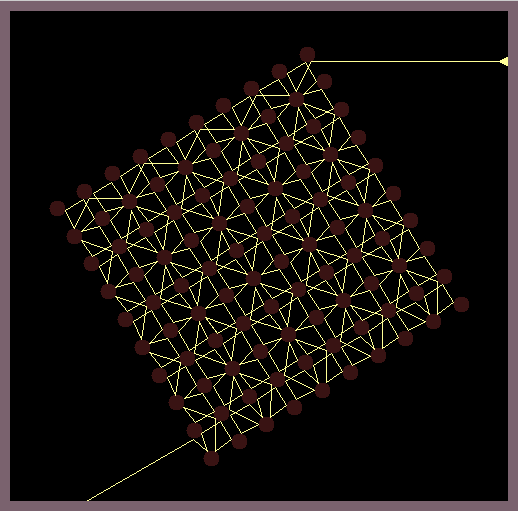
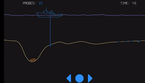
The software casts a light ray onto a grid of circular shaped mirrors and calculates all subsequent reflections by the law of geometric optics (the wave like nature of light is omitted). This simple model is very chaotic as errors of the position of the light source quickly blow up and indeed arbitrary precision math is needed to calculate most of reflection patterns.
The images in this gallery show symmetric reflection patterns emerging at special positions of the light source and special rotations of the mirroring lattice. Observe that the ray that leaves the light source (small triangle) enters the light source exactly at the same height on the backside.
The FroZenLight application is highly interactive and comes with a lot of predefined patterns.
FroZenLight - Ornament
FroZenLight - Cross
FroZenLight - Four Trees
FroZenLight - Cubistic Star
FroZenLight - Rock Crystals
FroZenLight - Patchwork
Une des principales caractéristiques du modèle en réseau simple de cercles est que toutes les structures de réflexion dépendent sensiblement des paramètres donnés, signifiant ainsi que le moindre changement peut avoir des effets spectaculaires. De grands nombres sont donc nécessaires pour révéler la beauté intrinsèque du modèle (voir la FroZenLight galerie).
Vous trouverez sur la page principale des exercices de mathématiques accompagnés de leurs solutions ainsi que d’autres documents.
