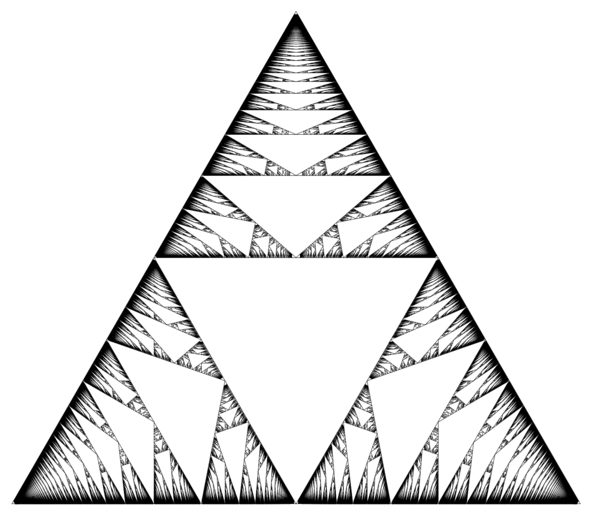
La baderne de Rauzy est dessinée en noir sur la première figure. Elle est liée à un développement en fraction continue exotique : à tout vecteur du simplexe standard dans ℝ³, on associe le vecteur obtenu en soustrayant les deux plus petites coordonnées de la plus grande et en renormalisant le vecteur obtenu (on ne reste dans le simplexe que si le vecteur ne satisfait pas l’inégalité triangulaire). La baderne de Rauzy est l’ensemble des points du simplexe pour lesquels cette opération peut être infiniment répétée.

Ces points apparaissent comme les vecteurs de fréquences possibles pour les suites de complexité 2n+1 qui n’admette qu’un seul mot de chaque longueur qui puisse être prolongé de plusieurs façons à gauche, et un seul mot de chaque longueur qui puisse être prolongé de plusieurs façons à droite.

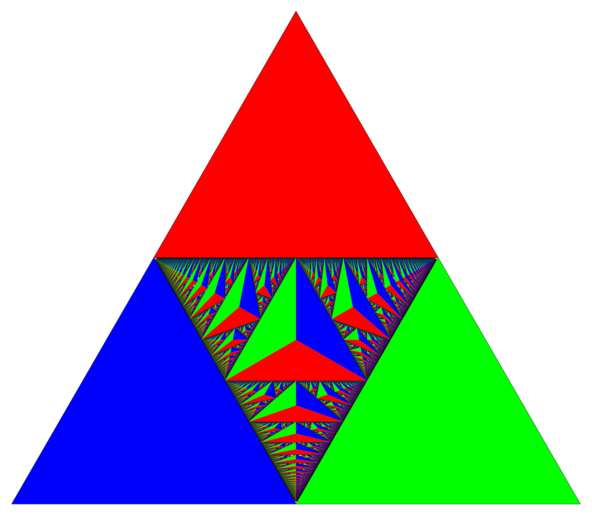
Avec un changement de coordonnées simple, le triangle de Rauzy apparaît aussi comme une sorte d’ensemble de Julia pour l’algorithme pleinement soustractif de développement en fraction continu, dual du précédent, qui consiste à retirer la plus petite des trois coordonnées aux deux autres. On sait depuis longtemps que, pour cet algorithme, presque tout point converge vers l’un des trois sommets, et on a représenté les trois bassins d’attraction des sommets et de leurs côtés adjacent en trois couleurs différentes; le complémentaire de ces bassins d’attraction est isomorphe à l’ensemble de Rauzy.

On sait que la mesure de Lebesgue de cet ensemble est nulle, mais on ne connaît pas sa dimension.