Algebraic Surfaces
I started playing with algebraic surfaces in the German Year of Mathematics 2008. This gallery shows a few results playing with the program SURFER.
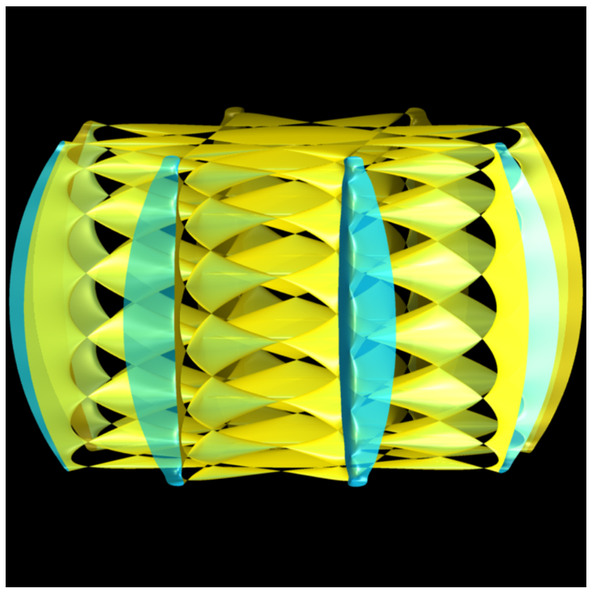
Sauermann Surface 255
a=0.5
256*a^8-512*a^6*x^2-512*a^6*y^2+320*a^4*x^4+640*a^4*x^2*y^2+320*a^4*y^4-64*a^2*x^6-192*a^2*x^4*y^2-192*a^2*x^2*y^4-64*a^2*y^6+64*x^6*y^2-128*x^4*y^4+64*x^2*y^6-16384*z^16+65536*z^14-106496*z^12+90112*z^10-42240*z^8+10752*z^6-1344*z^4+64*z^2-1

Sauermann Surface 255 - 3d Glasses

Formule
- (0.2*x^2+0.2*y^2+z^2-1)*(0.2*x^2+0.2*z^2+y^2-1)*(0.2*z^2+0.2*y^2+x^2-1)
4_x_sphere

Formule
- Plus: (x*y*z)^2*.009*(1.8-z)^2*(1.8+z)^2*(1.8-x)^2*(1.8+x)^2*(1.8-y)^2*(1.8+y)^2
4_x_sphere

Formule
- (0.2*x^2+0.2*y^2+z^2-1)*(0.2*x^2+0.2*z^2+y^2-1)*(0.2*z^2+0.2*y^2+x^2-1)+(x*y*z)^2*.009*(1.8-z)^2*(1.8+z)^2*(1.8-x)^2*(1.8+x)^2*(1.8-y)^2*(1.8+y)^2
4_x_sphere

Formule
- ((x^2+y^2+(z*1+ 0.45)^2-0.83)*(x^2+y^2+(z*1- 0.45)^2-0.83)*(x^2+y^2+(z)^2)*(x^2+y^2+(z)^2*(z)^2)*(x^2+y^2+(z- 0.45)^2-1)*(x^2+y^2+(z+ 0.45)^2-1)+(x+y)^2*(x-y)^2*(x*y)^2)
2_x_sphere

Formule
- (x^2+y^2+(z+0.45*-1)^2-1)*(x^2+y^2+(z-0.45*-1)^2-1)*((x+0.45*-1)^2+y^2+z^2-1)*((x-0.45*-1)^2+y^2+z^2-1)*(x^2+(y+0.45*-1)^2+z^2-1)*(x^2+(y-0.45*-1)^2+z^2-1)+(x*y*z)^2
6_x_sphere

Formule
- (x^2+(1*1.618034^2*x^2*1)+y^2+z^2-0.63)*(x^2+(1.618034^2*x^2)+y^2+z^2-1)*(x^2+y^2+(1*1.618034^2*y^2*1)+z^2-0.63)*(x^2+y^2+(1.618034^2*y^2)+z^2-1)*(x^2+y^2+z^2+(1*1.618034^2*z^2*1)-0.63)*(x^2+y^2+z^2+(1.618034^2*z^2)-1)+(x*y*z*7.31)^2
6_x_sphere

cube surface

Formule
- .805*(x^2 * (x^2+y^2+z^2-0.2^2) * (x^2+y^2+z^2-0.36^2)) + (y^2 * (x^2+y^2+z^2-0.6^2) * (x^2+y^2+z^2--0.36^2)) + (z^2 * (x^2+y^2+z^2-0.6^2) * (x^2+y^2+z^2-0.2^2)) + (x^2+y^2+z^2-0.6^2)*(x^2+y^2+z^2-0.2^2)*(x^2+y^2+z^2--0.36^2)*((x*9.11)^2+(y*9.11)^2+z^2-0.5619^2-0.36)

oktaederwuerfel

soft content 2011

Sunflower Sauermann 2008
a combination of two septics.
Original septic by Oliver Labs with 99
singularities.

Formule
- (x*(x^6-3*7*x^4*y^2+5*7*x^2*y^4-7*y^6)+7*z*((x^2+y^2)^3-2^3*z^2*(x^2+y^2)^2+2^4*z^4*(x^2+y^2))-2^6*z^7-(z+(49*a^2-7*a+50)*1)*((-12/7*a^2-384/49*a-8/7)*z^3+(-32/7*a^2+24/49*a-4)*z^2*1+(-4*a^2+24/49*a-4)*z*1^2+(-8/7*a^2+8/49*a-8/7)*1^3+(z+1)*(x^2+y^2))^2)*(-x*(x^6-3*7*x^4*y^2+5*7*x^2*y^4-7*y^6)+7*z*((x^2+y^2)^3-2^3*z^2*(x^2+y^2)^2+2^4*z^4*(x^2+y^2))-2^6*z^7-(z+(49*a^2-7*a+50)*1)*((-12/7*a^2-384/49*a-8/7)*z^3+(-32/7*a^2+24/49*a-4)*z^2*1+(-4*a^2+24/49*a-4)*z*1^2+(-8/7*a^2+8/49*a-8/7)*1^3+(z+1)*(x^2+y^2))^2)
Sunflower Sauermann 2008
A combination of two septics.
surfer Revision 55
Specail Surf-Code:
double PI = 2*arcsin(1);
root_finder=d_chain_newton;
epsilon=0.0000000000001;
iterations=1000;
iterations=1000;
a=2*a*(-0.140106854987124776454220549858);
clip=0;
Original septic by Oliver Labs with 99
singularities.

Sunflower Sauermann 2008 Centre
Sunflower Centre
surfer Revision 55
Specail Surf-Code:
double PI = 2*arcsin(1);
root_finder=d_chain_newton;
epsilon=0.0000000000001;
iterations=1000;
iterations=1000;
a=2*a*(-0.140106854987124776454220549858);
clip=0;
Original septic by Oliver Labs with 99
singularities.

Sauermann (?)
:-)
-64*x^6+64*x^4*y^4+8*x^4+64*x^2*y^2-8*x^2-64*y^6+8*y^4-8*y^2-1048576*z^22+5767168*z^20-13697024*z^18+18382848*z^16-15319040*z^14+8200192*z^12-2818816*z^10+604032*z^8-75504*z^6+4840*z^4-121*z^2+1

Sauermann Surface 2011
0.25*(x^2*y^2-x^2-y^2+1)*(x^4-2*x^2*y^2-4*x^2+y^4-4*y^2+4)+z*(z^2*((0.25*z^2-1.75)*z^2+3.5)-1.75)-0.5

fivegon is based on the Tschebyscheff -Polynomial
x^5-10*x^3*y^2-5*(x^2+y^2)^2+20*(x^2+y^2)+5*x*y^4+8*(0.5*z^7-3.5*z^5+7*z^3-3.5*z-1)-16

kubismus sauermann 2011

3 x sphere Sauermann

Sauermann Surface 112 Nodes

Sauermann Surface Nodes 72

Sauermann Surface2013
-(z+1)*(z^4-5*z^3+6*z^2+z-2)^2+(x^2-1)*(y^2-1)*(x^4-2*x^2*(y^2+2)+y^4-4*y^2+4)

Another Sauermann Surface 2013

Another fivegon is based on the Tschebyscheff -Polynomial

Sauermann Nonic Surface 2013

Nonic Surface Demo

Sauermann nodal cubic surface
x^3+3*x^2*(-1+y)-3*y^2-3*x* y^2-y^3+(1+z)*(1+2*z-4*z^2)^2

Sauermann Surface
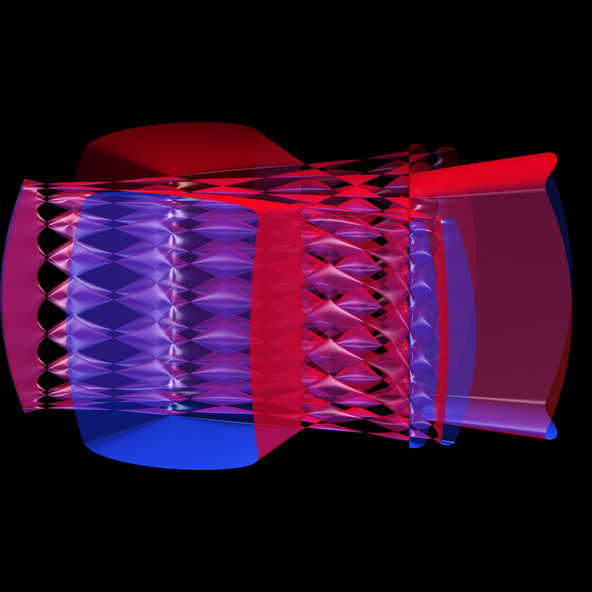
Sauermann d9 T9 Demo

Sauermann Surface 2013
(x-y-1)*(x+y-1)*(x^2-2*x*(2*y+1)+(y-2)*y-2)*(x^2+x*(4*y-2)+y*(y+2)-2)+128*(z^5-1.25*z^3+0.3125*z)^2

Sauermann Surface II 2013

d=12 Demo Sauermann 2013
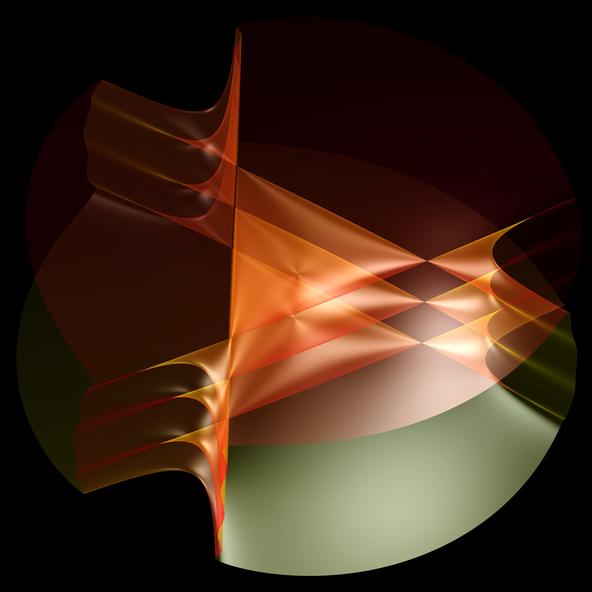
d=3 Demo Sauermann 2013

d=3 Demo Sauermann 2013

d=10 Demo Sauermann 2013
2+20*x+30*x^2-120*x^3-30*x^4+196*x^5-70*x^6-80*x^7+70*x^8-20*x^9+2*x^10-30*y^2-120*x*y^2-300*x^2*y^2+440*x^3*y^2+650*x^4*y^2-720*x^5*y^2-280*x^6*y^2+400*x^7*y^2-90*x^8*y^2+130*y^4+180*x*y^4+550*x^2*y^4+400*x^3*y^4-700*x^4*y^4-280*x^5*y^4+420*x^6*y^4-170*y^6-240*x*y^6-280*x^2*y^6-560*x^3*y^6-420*x^4*y^6+70*y^8+140*x*y^8+90*x^2*y^8-2*y^10-72*z^2+192*z^4-128*z^6































































































