The Heidelberg Laureate Forum Foundation invites you to visit the exhibition “Mathematics of Planet Earth” at Karlstorbahnhof in Heidelberg, Germany! It runs from July 5 to Aug 2, 2015, for the first time in Heidelberg. It offers a big variety of exciting adventures for children and adults alike.
Jos Leys, Étienne Ghys et Aurélien Alvarez
Les images suivantes sont extraites en haute résolution de deux chapitres du film «Dimensions, une promenade mathématique». Dans un chapitre, Hipparque nous montre comment décrire la position d’un point quelconque sur la Terre à l’aide de deux nombres et nous explique la projection stéréographique. Dans un autre chapitre, le mathématicien Ludwig Schläfli parle d’objets à quatre dimensions et nous montre un défilé de polytopes de dimension 4, étranges objets avec 24, 120 voire même 600 faces ! Deux autres images du film ressemblant à des noeuds sont remarquables.
Le Hécatonicosachore
Également appelé le «120-cellules», le hécatonicosachore est un polytope régulier en dimension 4. C’est l’analogue en dimension 4 du dodécahèdre (12 faces pentagonales, 20 sommets et 30 arêtes) en dimension 3.
Le hécatonicosachore a 120 «faces», mais elles sont en réalité tri-dimensionnelles dans l’espace de dimension 4: chacune d’elles est un dodécahèdre ! Les faces bi-dimensionnelles de ces dodécahèdres sont bien sûr des pentagones, ils sont en tout 720. On compte également 600 sommets et 1200 arêtes.
Le Hécatonicosachore (intérieur)
Les images du film montrent le 120-cellules représenté au moyen d’une projection stéréographique, qui n’est pas la représentation stéréographique habituelle d’une sphère de l’espace de dimension 3 vers un plan passant par le pôle sud de celle-ci. Il s’agit en fait de la projection stéréographique d’une sphère de l’espace de dimension 4 vers notre espace à trois dimensions.
Cette projection montre très clairement les symétries du 120-cellules. Notons aussi que les faces bi-dimensionnelles de cet objet sont des parties de sphères et que les arêtes sont des arcs de cercles.
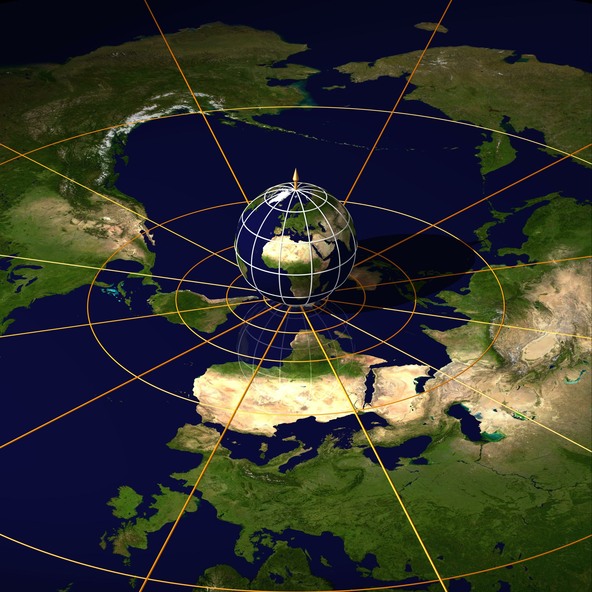
Projection stéréographique
Les points d’une sphère sont projetés à partir du pôle nord sur un plan perpendiculaire à l’axe des pôles, généralement le plan passant par le pôle sud. Tous les points de la sphère peuvent ainsi être projetés sur ce plan, excepté le pôle nord lui-même. On associe alors un point à l’infini au pôle nord.
La projection stéréographique projette les cercles de la sphère en des cercles du plan tout en conservant les angles.
Matrice réelle
Expliquer cette image en quelques lignes est bien difficile. Pour plus d’informations, voire cet article.
Flot d'Anosov
Expliquer cette image en quelques lignes est bien difficile. Pour plus d’informations, voire cet article.