Die Stiftung Heidelberg Laureate Forum Foundation lädt Sie vom 5. Juli bis 2. August 2015 im Karlstorbahnhof Heidelberg ein, die Ausstellung „Mathematik des Planeten Erde“ zu besuchen. Die Ausstellung ist zum ersten Mal in Heidelberg und verspricht für Jung und Alt ein abwechslungsreiches und spannendes Erlebnis.
Jos Leys, Étienne Ghys and Aurélien Alvarez
Galerie
Jos Leys, Étienne Ghys and Aurélien Alvarez
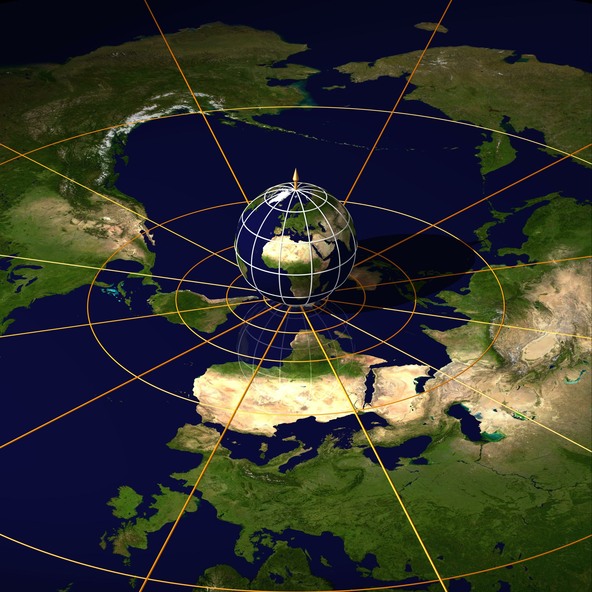
Die Ausstellung IMAGINARY zeigte die erste Vorstellung von „Dimensionen, ein Spaziergang durch die Mathematik”, ein Film von Jos Leys, Étienne Ghys und Aurélien Alvarez. Der Film ist nicht nur etwas für MathematikerInnen, sondern spricht ein breites Publikum an, und versucht in neun Abschnitten, den Begriff der vierten Dimension zu erklären. Er kann gratis für den nicht-kommerziellen Gebrauch heruntergeladen werden. Die folgenden Abbildungen sind Bilder aus zwei Abschnitten des Films mit hoher Auflösung. In einem Kapitel zeigt uns Hipparchos, wie die Lage eines Punktes auf der Erde mit zwei Zahlen zu beschreiben ist und erklärt die stereografische Projektion. In einem weiteren Kapitel spricht der Mathematiker Ludwig Schläfli über Objekte, die in der vierten Dimension leben, und zeigt eine Parade vierdimensionaler Polytope, fremdartige Objekte mit 24, 120 und sogar 600 Seiten. Zwei Bilder der Ausstellung, die wie Knoten aussehen, sind ganz besonders. Eine visuelle Einführung dazu geben Jos Leys und Étienne Ghys in einem Artikel der amerikanischen mathematischen Gesellschaft.
Links
http://www.dimensions-math.org
http://www. ams.org/featurecolumn/archive/lorenz.html
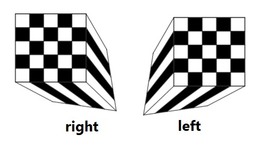
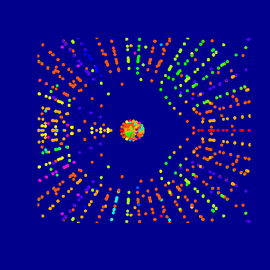
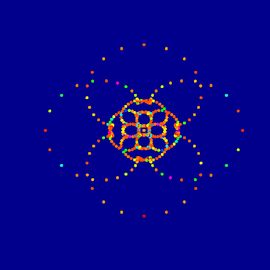
Das Hecatonicosachoron
Das Hecatonicosachoron ist ein reguläres Polytop (Vieleck) in vier Dimensionen und wird auch die „120-Zelle“ genannt. Es ist das 4-dimensionale Analogon des 3-dimensionalen Dodekaeders, das 12 fünfeckige Seitenflächen, 20 Ecken und 30 Kanten hat. Das Hecatonicosachoron hat 120 „Seitenflächen“ im Vierdimensionalen, das heißt sie sind eigentlich 3-dimensionale „Flächen“, also Dodekaeder! Die 2-dimensionalen Flächen dieser Dodekaeder sind Fünfecke, insgesamt 720. Es gibt 600 Ecken und 1200 Kanten.
Lizenz CC BY-NC-SA-3.0
Das Hecatonicosachoron (Fortsetzung)
Die Bilder zeigen die 120-Zelle in stereographischer Projektion einmal von innen und einmal von außen. Es ist aber nicht die Projektion von einer Kugel auf die Ebene durch den Südpol, sondern die Projektion einer 3-dimensionalen Kugel im vierdimensionalen Raum in den 3-dimensionalen Raum. Die Projektion zeigt die Symmetrien der 120-Zelle sehr gut. Wie man sehen kann, sind die zwei-dimensionalen Flächen des Objektes alle Teile von Kugeln und die Ecken Kreissegmente.
Stereographische Projektion
Punkte auf einer Kugel (Sphäre) werden vom Nordpol aus auf eine Ebene projiziert, die rechtwinkelig zu der Pol-Achse liegt. Normalerweise ist das die Ebene die durch den Südpol geht. Alle Punkte der Kugel können so auf die Ebene projiziert werden, bis auf den Nordpol selbst. Man nimmt daher einen unendlich weit entfernten Punkt zur Ebene hinzu. Dieser repräsentiert den Nordpol. Die stereographische Projektion bildet Kreise auf der Kugel auf Kreise in der Ebene ab. Winkel von sich schneidenden Kreisen bleiben dabei erhalten.
Lizenz CC BY-NC-SA-3.0
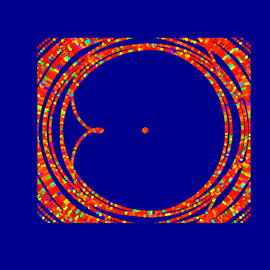
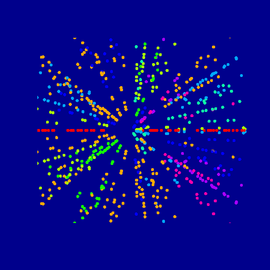
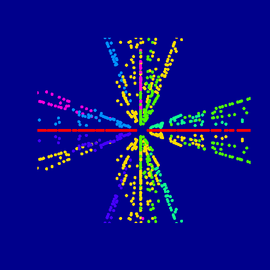
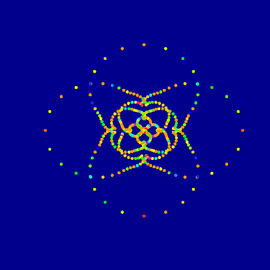
Anosov-Fluss und reelle Matrix
Es ist schwierig, diese Bilder in wenigen Zeilen im Detail zu erklären. Mehr Informationen dazu gibt es unter:
Anosov-Fluss und reelle Matrix (Fortsetzung)
Dynamik ist die Lehre der Bewegung. Topologie ist die Lehre der Formen. Arithmetik ist die Lehre der Zahlen. Manchmal haben Objekte aus der Arithmetik dynamische Aspekte und erzeugen interessante Formen! Auf diesen beiden Bildern werden Formen durch den so genannten „modularen Fluss“ erzeugt. Dieser ist fundamental wichtig, um Zahlen zu verstehen, speziell die Primzahlen.
Lizenz CC BY-NC-SA-3.0