Saturn.
From a mathematical point of view, Saturn is not much more than a sphere with a plane crossing it in the middle.
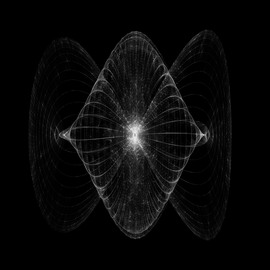
Then to see this planet appear, we need a sphere (x2+y2+z2-30=0 for example), and a plane (y=0 for example). Thus the points of the space that satisfy y(x2+y2+z2-30)=0 are not on Earth, are not on Mars, but are on Saturn!
The first image of this gallery is the surface defined by this equation.
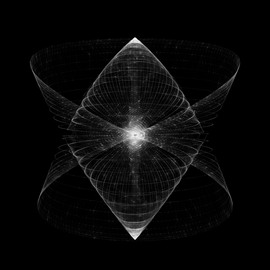
One can say “But a planet is not a “perfect sphere”!” and this person would be right. Well, in fact it’s more an ellipsoid than a sphere. So we just have to adjust the equation of the sphere x2+y2+z2-30=0 to make it an ellipsoid 0,6x2+0,8y2+z2-30=0. Then if you draw y(0,6x2+0,8y2+z2-30)=0, you will see the second image of this gallery. An ellipsoid with a plane crossing it in the middle. It is a “better” Saturn than the first one.
Now, one can say “but the rings of Saturn are not a plane, they are not touching the ellipsoid!”, and this person would be right. Again. Well now it’s a bit more complicated, but if you draw ((0.2x2+0.4y2+z2+0.12)2-0.5(0.2x2+0.4y2))*(0.4x2+0.6y2+0.6z2-0.1)=0 you will see the last image of this gallery.
Now one can say “We can do better!”, and this person would be right. Again. But this time I let you play with SURFER, the software I used to create these images, to do a better Saturn!
The only certainty is that nobody can do a perfect Saturn!