Stepan Tersian, Gallery I
Eight photos and seven pictures are included in the Gallery I. They are inspired by my visit at Faculty of Mathematics, University of Santiago de Compostela, Spain. I saw and I was wondered by the exhibition IMAGINARY in Santiago.
I made four compositions with surfaces by Mathematics software Mathematica and Maple and complete them by graphs of curves and two math problems. Eight photos with mathematical content from Santiago de Compostela, A Coruna, Baiona and Tryavna are presented as well.

The tree of sciences at University of Santiago de Compostela

Atlas with Sphere, Toral square, Santiago de Compostela
A stone figure, presented as Atlas, of Bendana palace (Pazo Bendaña) located at the Toral square in the historic area of Santiago de Compostela. Atlas keep a Sphere on its shoulders adorned with the sun and stars. The Eugenio Granell Foundation and Museum is housed in Bendana palace by 1995. Eugenio Granell (1912-2001) is a surrealist painter and artist, who was born in A Coruna, and spent his childhood and youth in Santiago de Compostela.

On the tower of Hercules, A Coruna

Triple helix spiral staircase in the Museum do Pobo Galego
Unique triple helix spiral staircase in the Museum of Galician People (Museo do Pobo Galego) ), Santiago de Compostela.

Spiral staircase 2

Perspective, Baiona

May Sun wood carved ceiling , Daskalov house 1808, Tryavna, Bulgaria
The unique Wood-Carving Museum in Bulgaria is housed in the old Daskalov’s House in town of Tryavna. It was built by the merchant Hristo Daskalov from 1804 to 1808. The two carved Suns on the ceilings in two of the rooms are the most famous exhibits. They were made by the master Dimitar Oshanetsa and his scholar Ivan Bochukovetsa, during a period of six months in 1808. They were in competition to who one of them would decorate a ceiling with wood-carvings more beautifully. The carvings have geometry symbolizing calm May and hot July Suns.

July Sun wood carved ceiling , Daskalov house 1808, Tryavna, Bulgaria

Fruits 1
Cup: x2+y2=16z4
Apple: (x2+y2+z2)2= x2+y2
Lemon: x2+z2=4y3(1-y)3 , made by Maple.

Lemons and Figs 1
Plots of surfaces:
x2+y2=4z3(1-z)2 and x2+y2=64z4(1+z)3,
made by Mathematica, using ParametricPlot3D.

Fruits 2
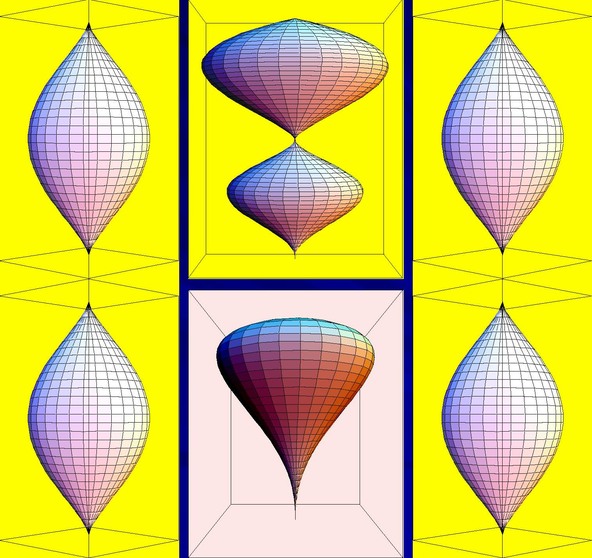
Lemons and Figs 2
Plots of surfaces:
x2+y2=4z3(1-z)3 (lemon),
x2+y2=4z5(1-z) (fig) and x2+y2=4z2(1-z)5,
made by Mathematica, using ParametricPlot3D.

Circles and ellipses
8 circles with radius r=1.6, CK: {Cos[2πk/n]+r Cos[t], Sin[2πk/n]+r Sin[t]},
{t,0,2 π}, k=1,…, 8, n=8.
8 ellipses with semi axes a=1.6, b=1.2 , {t,0,2 π}, k=1,…, 8, n=8.
E_K:{Cos[2πk/n]+a Cos[2πk/n] Cos[t] +b Sin[2πk/n] Sin[t],
Sin[2πk/n] - a Sin[2πk/n] Cos[t] +b Cos[2πk/n] Sin[t]}.

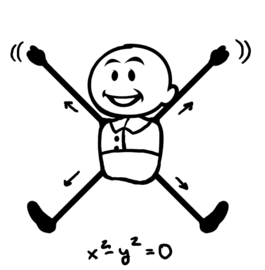
Two problems
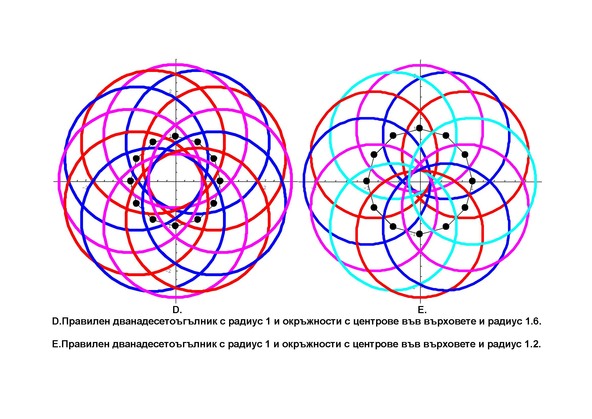
Circles
12 circles with radius r=1.2 in three and four colors
Ck: {Cos[2πk/n]+r Cos[t], Sin[2πk/n]+r Sin[t]}, {t,0,2 π},
k=1,…, 12, n=12.