A few examples of stochastic processes from physics and biology
The images in this gallery are mostly simulations of stochastic processes, arising from applications in statistical physics or in biology. A stochastic process is a process evolving in time in a random way. Thus it can also be seen as a family of random variables indexed by time. Typical examples are the size of a population, the boundary between two phases in an alloy, or interacting molecules at positive temperature.
The programs generating these images have been coded directly in C, which is used to produce eps files, which can then be translated into other formats. There are also a couple of related movies in the films section.
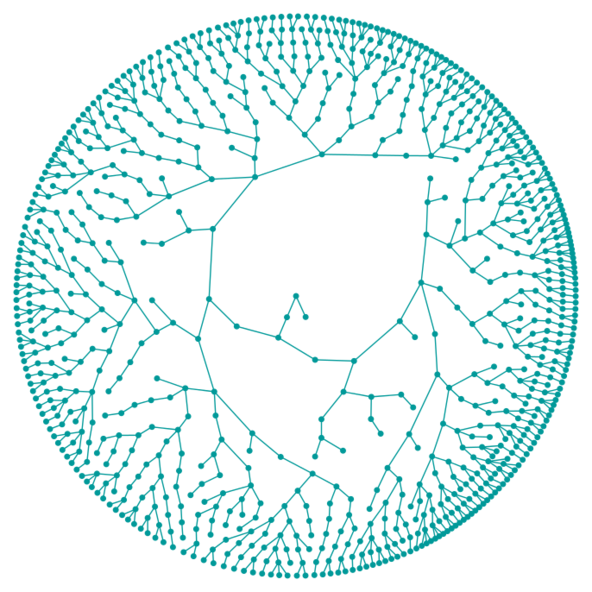
Galton-Watson tree
A realisation of a Galton-Watson tree. The ancestor, in the center of the picture, has two children. Each individual has again a random number of children (between 0 and 3 in this simulation), all children numbers being independent and identically distributed.
Une réalisation d’un arbre de Bienaymé-Galton-Watson. L’ancêtre, au centre de l’image, a deux enfants. Chaque individu a à nouveau un nombre aléatoire d’enfants (entre 0 et 3 dans cette simulation), tous les nombres d’enfants étant indépendants et identiquement distribués.
Pour une explication détaillée, voir http://images. math. cnrs.fr/La-probabilite-d-extinction-d-une.html
Bond percolation
A realisation of bond percolation on a subset of Z2 (p = 0.525).
Each edge is open with probability p. Dark edges form the connected component of the lower boundary.
Une réalisation d’une percolation de lien sur une partie de Z2 (p = 0.525).
Chaque lien est ouvert avec probabilité p. Les liens foncés forment la composante connexe du bord inférieur.
Surface growth model
Particles fall randomly and get stuck as soon as they touch another particle below or sideways. The scaling limit of this model is governed by the KPZ equation.
Des particules tombent de manière aléatoire et restent figées dès qu’elles touchent une autre particule en dessous ou sur les côtés. La limite d’échelle de ce modèle est gouvernée par l’équation KPZ.
Voir aussi http://images. math. cnrs.fr/Qu-est-ce-qu-une-Equation-aux.html
Stochastic Allen-Cahn equation
The stochastic Allen-Cahn equation describes phase separation in an alloy.
L’équation d’Allen-Cahn stochastique décrit la séparation de phases dans un alliage.
Voir aussi http://images. math. cnrs.fr/Qu-est-ce-qu-une-Equation-aux.html
