A few examples of stochastic processes from physics and biology
갤러리
A few examples of stochastic processes from physics and biology
이 갤러리의 이미지는 대부분 통계물리학이나 생물학의 응용수학에서 발생하는 확률 과정의 시뮬레이션입니다. 확률과정이란 시간에 따라 무작위로 변화하는 과정으로, 시간에 따른 확률변수의 시계열로 간주될 수 있습니다. 전형적인 예는 인구 수, 합금 두 상 사이 의 경계, 또는 양의 온도에서 상호 작용하는 분자들이 있습니다.
이러한 이미지를 생성하는 프로그램들은 C언어로 짜여졌고, 다른 포맷으로 변환될 수 있는 .eps 파일을 생성합니다. 영상(films) 코너에서 관련된 동영상들을 감상하세요.
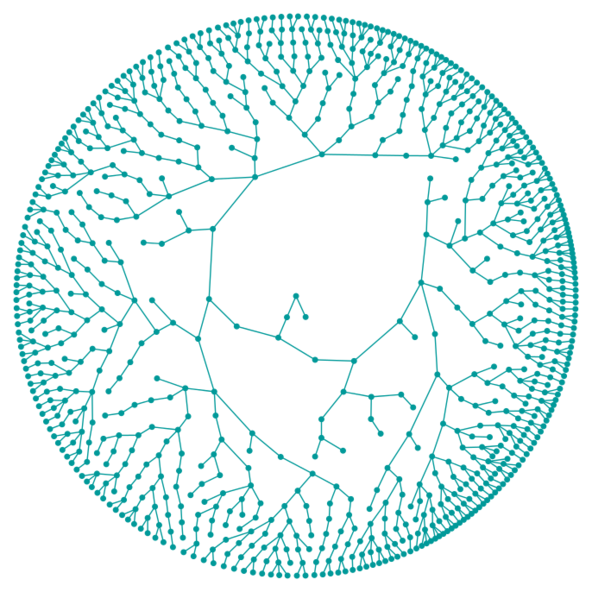
Galton-Watson tree
Galton-Watson tree의 구현입니다. 그림의 중심에는 최초의 공통 조상이 2개 자손을 갖고 있습니다. 각 개체의 자손 수는 (0에서 3 사이의) 상호독립적인 같은 분포를 갖습니다.
자세한 설명은 http://images. math. cnrs.fr/La-probabilite-d-extinction-d-une.html 을 참조하세요. (프랑스어)
저작권 CC BY-NC-SA-3.0