Jean Constant - Fractals
The term fractal was first used by mathematician Benoît Mandelbrot. The geometric characterization of a fractal is self-similarity as the original shape is made of smaller copies of itself. Fractal patterns can be found in the environment in trees, rivers, and many other forms. Minimal surfaces, on the opposite, are completely self contained objects of a more abstract nature.
How do two fundamental mathematical concepts can enhance each other in a graphic environment was the purpose of this study. The following are two examples of a 30 images portfolio on fractal and minimal surfaces available at hermay.org
The fractals were generated in Chaos Pro & U&I Software, ArtMatic. The surfaces were composed in 3DXplorMath.
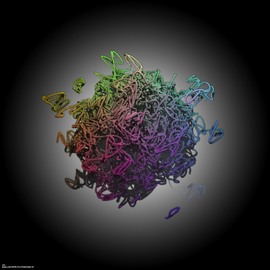
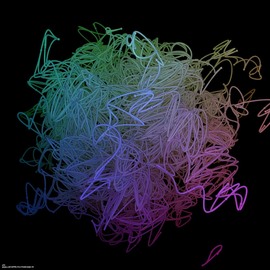
Fractal #01
The splicing of a larger fractal function was used as a background.
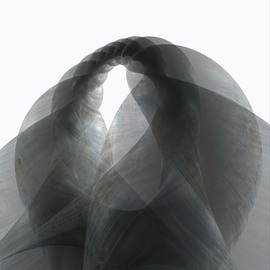
Several conoids, part of the larger family of parametric surfaces were created in 3DXplorMath and added in various size and position to emphasize the expansionary character of the fractal.
Fractal #02
Close up of a fragment of fractal function generated in UISoftware.
The wireframe of a Wilmore surface with dihedral symmetry pseudosphere eversionwas created in 3DXPlorMath, distorted and manipulated in a raster graphic program to complement the dynamic of the fractal image.
This image was selected to promote a series of Mathematics and Art exhibitions in several universities and cultural centers in Europe.
