Hand made hands-on
여기에 등장하는 체험활동 전시물들은 독일 누렘베르크(Nuremberg)에서 열린 다음 세 전시 Form & Formel (2008), Keplers Formen (2009), and Die quasiperiodischen Formen (2011)에서 온 것들입니다. 모든 전시물들은 Uli Gaenshirt에 의해 고안되고 제작되었고, 그는 또한 이 전시들의 아이디어 및 컨셉을 제안하여 KOMM-Bildungsbereich와 함께 전시회가 개최되었습니다.
피타고라스 정리의 공간 모형
세 변의 길이의 비가 3:4:5인 삼각형은 직각삼각형입니다. 왜냐하면 세 수 3^2 + 4^2 = 5^2가 피타고라스 정리의 등식 a^2 + b^2 = c^2을 만족시키기 때문입니다.
배경의 하얀색 물체는 파라오 쿠푸(Khufu)의 피라미드의 왕의 방(King’s Chamber)의 축소 모형입니다. 놀랍게도, 12개의 매듭이 있는 끈으로 만들어진 빨간 3-4-5 삼각형이 내부공간 안에 정확히 들어갈 수 있습니다.
전면의 물체는 피타고라스 정리의 공간 막대 모형(Spatial Pythagorean Stick Model)입니다. 수직 방향의 고정된 막대기에는 3개의 빨강, 초록, 파랑 구슬이 각각 높이 7, 8, 9단위에 박혀 있습니다. 몇 개의 구슬들은 피타고라스 등식의 가능한 정수해를 기준으로 평면에 추가로 박혀 있습니다. 단위길이가 표시되어 제공되는 막대기들은 정수 대각선들의 길이와 일치하게 만들어졌습니다.
공간의 데카르트 좌표계(Cartesian coordinate system), 즉, 직교좌표계에서 점 P0 (0,0,0)과 다른 점 P1 (x,y,z) 사이의 거리 d는 공식 x^2 + y^2 + z^2 = d^2 로 주어집니다.
등식 12^2 + 20^2 + 9^2 = 25^2 에 맞추어, 소녀는 두 파란 구슬을 잇는 정확한 길이의 막대기를 선택했습니다.
피타고라스 정리의 구형 모형
청년이 피타고라스 정리의 구형 모형(Pythagorean Sphere Model)의 활을 움직이고 있습니다. 내부에 검은 선으로 표시된 원의 부분은 반지름 65cm의 구에 접합니다.
이 검은 선이 스치고 지나가는 나무 직육면체들의 꼭지점들은 등식 x^2 + y^2 + z^2 = 65^2의 정수해에 대응됩니다. 실제로 꼭지점 P (15|36|52) 와 만나게 됩니다.
반지름이 65인 구 전체에선 342개의 정수 좌표를 가진 점들을 찾을 수 있습니다.
이 모형에는 120AD 경의 로마의 판테온(Pantheon)이 영향을 주었습니다. 특히 내부공간에 완벽히 들어가는 구의 모습과 89개의 정사각형들이 바닥에 채워져서 16개의 꼭지점에서 만나는 바닥 문양 이 두 가지가 영향을 주었습니다. 이 바닥 문양 디자인은 11 x 3과 7 x 9 크기의 두 개의 직사각형들을 겹쳐 바닥을 깐 것으로, 등식 11^2 + 3^2 = 7^2 + 9^2 에 의해 이 두 직사각형들의 대각선 길이는 같습니다.
쿠푸 왕의 피라미드의 기하학
피라미드의 4개의 변들은 늘여진 빨간 실들입니다. 까만 삼각형이 피라미드 면의 경사를 알려줍니다. 삼각형의 수평인 변 a와 수직한 변 b의 비는 11:14입니다. a의 값은 보통 220 이집트 로얄 큐빗(Egyptian royal cubits)인 115.19m로 정해지고, 이로 계산한 b는 146.60 m 혹은 280 로얄 큐빗입니다.
이 모형은 황금비 τ (τ = 1.61803…)와 원주율 π (π = 3.14159…)을 이용해 다른 방식으로 높이 bτ 와 bπ 을 구하는 방식을 보여줍니다.
b(τ) = (τ^0.5) a = 146.52 m
b(π) = 4 (π^-1) a = 146.66 m
(주의 사항: τ^0.5 = √τ 그리고: π^-1 = 1/π )
고대의 측량 기술로는 b, bτ, bπ 이 세 값 사이의 차이를 찾을 수 없었습니다. 아마도 피라미드는 근본적으로 기하학적인 건축이라고 생각되었을 것입니다.
현수선과 포물선
늘어진 사슬의 모양은 현수선(catenary)이라 불립니다. 이 곡선의 대수학적 표현은 y축에 대해 대칭인 두 식 y = 0.5 (e^x) 와 y = 0.5 (e^-x) 의 합으로 이루어집니다. (e = 2.71828…)
만약 우리가 현수교에서처럼 늘어진 선에 등거리의 선으로 이루어진 동일한 하중을 추가한다면, 선의 모양은 보다 뾰족한 포물선(parabola)으로 바뀔 것입니다.
이 변형은 늘어진 선의 가운데에는 다른 곳에 비해서 하중을 주는 더 많은 접점이 붙어 있다는 것을 생각하면 쉽게 이해할 수 있습니다. 가운데 부분에는 더 많은 무게가 실려서 더욱 뾰족한 모양이 되고, 바깥 부분에 적게 실리는 무게는 균일한 무게를 지닌 사슬에 비해 실이 더 늘어진 모양을 하게 합니다.
타원의 역학
I. 철제 고리로 표시된 관측 구멍에서 보면, 하얀 전체 타원이 아크릴 플렉시글라스에 보이는 검은 원을 정확히 채우게 됩니다. 즉 관측 구멍과 원이 이루는 원뿔의 단면이 타원이 됩니다.
II. 천문학자 요하네스 케플러(Johannes Kepler, 1571-1630)는 두 동심원의 반지름 선분으로 주어지는 교점의 사영으로 타원을 그려냈습니다. 반지름 선분이 내부의 동심원과 만나는 교차점에서 수평선을, 외부의 동심원과 만나는 교차점에서 수직선을 긋습니다. 이 둘의 교차점들을 모두 이으면 타원이 완성됩니다. 좌상단의 교차하는 끈들을 (타원과) 비교해 보세요.
III: 정수좌표 점들의 예를 이용하여 타원이 원을 수평 방향으로 늘인 것을 볼 수 있습니다.
IV. 타원 컴퍼스(ellipsograph)는 미끄러지는 받침대에 놓여 움직일 수 있는 막대기를 이용해서, 두 초점에 끝점이 연결되어 있는 선으로 만들어진 타원을 그려냅니다.
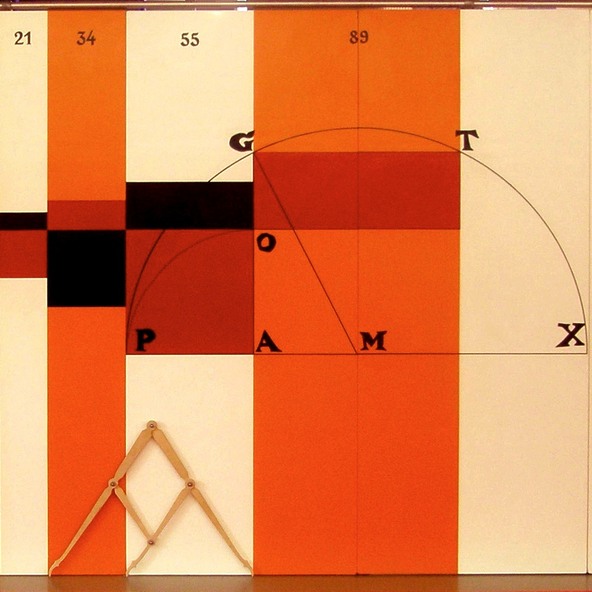
케플러의 황금비 해석
요하네스 케플러(Johannes Kepler)의 디자인인 목판 위에 검은색으로 그려진 도형은, GA = 2 AM 인직각삼각형 GAM의 밑변을 기준으로 어떻게 황금비 OA:GO = GA:OA 를 만들어 내는지 보여줍니다. 정확한 그림에서라면 정사각형 AOP와 직사각형 GOT의 넓이는 동일해야 합니다.
현대에 황금비는 보통 τ = 0.5 (√5 - 1) = 1,6180339887… . 로 정의됩니다. 한편 OA:GO = GA:OA = τ 라는 사실을 참고하세요.
케플러의 목판 위에 나타난 정사각형과 직사각형들의 나열들은 피보나치 수에 의존하고 있습니다. 이는 초기조건 F0 = 0 과 F1 = 1을 갖고 Fn+2 = Fn+1 + Fn 의 점화식으로 정의된 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, … 로 나아가는 수열입니다. 케플러의 공식 Fn+1 · Fn+1 = Fn · Fn+2 +(-1)^n 은 n이 무한대로 갈 때 비율 Fn+1 : Fn 이 τ로 수렴함을 말해줍니다. 예로 n이 9일 때는 큰 빨간색의 사각형 (넓이 3025 cm^2 = 55 cm · 55 cm) 과 큰 빨간색의 직사각형 (3026 cm^2 = 34 cm · 89 cm)의 넓이는 거의 동일합니다.
이 비율에서 나오는 분수들로 황금비에 대한 근사식을 증명할 수 있습니다.
Icosahedral Mirrors with inlaid Hexagon
상감 육각형이 20 번 나타나는이 거울 물체는 어린이와 성인에게 매우 인기가 있습니다.
물체는 밑면 대 높이 비율이 1 : 0.5 τ (τ = 0.5 (√5 + 1) = 1.61803 …) 인 이등변 삼각형 형태의 세 개의 거울로 구성됩니다. 이 거울 물체는 나무로 만들어져 있습니다.
거울의 똑같이 긴 측면은 서로 연결되어 있으며 각각 72°의 내부 각도를 형성합니다. 결과적으로 육각형에 부착 된 검은 색 줄무늬가 오각형으로 나타납니다. 여러 예금자가 제공됩니다.
이 갤러리의 일부 개체는 2016 년 6 월 뉘른베르크에서 처음으로 전시 된 “IMAGINARY - Form und Formel mathematischer Fantasie”전시회에 자세히 설명되어 있습니다.
대입과 사영
이 대상은 황금비 τ = 0.5 (√5 - 1) = 1.61803… 를 이용한 준주기(quasiperiodic) 수열을 만드는 두 가지 다른 방법을 보여줍니다.
위쪽의 막대에는 대입 방법(substitution method)이 묘사됩니다. 막대의 첫 번째 열에서 긴 파란색 구간 Lq와 짧은 주황색 구간 Sq의 길이 비율은 τ : 1입니다. 두 번째 열에서 이 둘 Lq 와 Sq는 더 작은 구간들로 대체되는데, L = Lq · τ^-3 and S = Sq · τ^-3 (메모: τ^-3 = 1/(τ^3) = 0.236…) 로 잡았을 때 Lq → L + S + L + S + L and Sq → L + S + L 이런 식으로 대체됩니다. 셋째 열에서 한번 더 반복을 통해 얻은 구간 L’과 S’는 역시 τ -3의 비율로 줄어듭니다.
준주기 수열을 만드는 또 다른 방법은 띠 사영 방법(stripe projection method)으로 불립니다. 노란 판의 정사각 격자의 경사각 φ는 tan φ = τ로 주어집니다. 수평 방향의 빨강/주황 줄무늬 속의 점들의 수직 사영은 대입 방법으로 얻어낸 수열과 완전히 일치하게 대응됩니다.
준단위(quasi-cell)로 통제되는 피보나치의 토끼
13세기 초에 피보나치(Leonardo Fibonacci)는 토끼 집단의 개체수를 계산하는 가상의 규칙을 서술하였습니다. 이 규칙은 어린 토끼들의 쌍과 어른 토끼들의 쌍들에 대한 준주기(quasiperiodic) 수열을 만들어 냅니다. 길이 S를 어린 토끼들의 쌍에, 길이 L을 어른 토끼들의 쌍에 대응시키면, 수열은 대입 방법에 의해 만들어진 것과 정확히 일치합니다.
사진 위쪽에 보이는 일차원의 준단위(quasi-cell)들이 순차적으로 준주기 수열을 만들어 갑니다. 노란색 미끄럼자들이 이어지는 성장을 결정합니다. 자들은 주기적인 평균 길이를 갖고 있습니다. 사진에서 보듯 이들의 끝점을 서로 연결하면, 준단위들의 작동 방식이 이 완벽한 준주기 수열을 성장시키는 원동력이 됩니다.
이 1차원 준단위는, 다음 세 체험물들의 주제인 빈틈 없는 10각형의 준결정 성장의 모형을 만드는 기초가 됩니다. 더욱 자세한 정보는 Wickerwork 갤러리 설명서(description booklet of the Wickerwork gallery, 독어/영어 제공)에서 찾아볼 수 있습니다.
펜로즈(Penrose) 마름모로 만든 수레바퀴
파란 십각형 위에 그려진 Ammann 격자는 수평으로 확장된 경계선을 가진 수직 피보나치 수열에 기초해 있습니다. 수직 피보나치 수열의 일차원 격자는 36°의 배수만큼 돌려진 4개의 복사본과 같이 비대칭적으로 중첩되어 놓여 Ammann 격자를 만들게 됩니다.
두꺼운 하얀색 도형과 보다 작은 노란 색조의 도형들이 십각형의 중심에 자석으로 고정되어 있는데, 이들은 펜로즈 마름모(Penrose rhomb)라 불리고 Ammann 격자의 절단으로 표시되어 있습니다. 이 펜로즈 마름모들의 “짝짓기 규칙”(matching rules)들이 이 선들이 마름모에서 마름모로 이어지게 뻗어나가는 방식을 결정합니다.
이렇게 펜로즈 타일링(Penrose tiling)이 마름모의 표시들이 십각형의 Ammann 격자에 연관딜 때 “수레바퀴”(cartwheel)라 불립니다. 하지만 위쪽의 두 검은 경계선의 마름모들은 짝짓기 규칙을 따르지 않으므로 “수레바퀴 체계”(cartwheel order)에 속하지 않습니다. 자유롭게 맞춰지는 펜로즈 타일링은 언젠가 짝짓기 규칙을 위반해야 한다는 사실을 증명할 수 있습니다. 아래쪽의 두 검은 경계선의 마름모들은 다른 타일 방법에 따라선 바르게 맞춰질 수 있는 마름모들입니다.
Q 준단위체(Quasi-cell Q)
준결정의 성장의 수학적 표현을 펜로즈 마름모들의 짝짓기 규칙이나 관련된 번갈아 겹치는 단위체(Gummelt의 십각형)의 덮개 규칙(covering rules)만으로 설명하려면 항상 맞지 않는 부분이 생기게 됩니다.
준주기 연쇄(quasiperiodic succession) 알고리즘도 순차적으로 작동하지만, 이는 각각의 준단위체 Q에 대한 두꺼운 마름모들을 조절하여 빈틈없는 수레바퀴 체계의 성장을 촉진시킵니다.
준단위체 Q에 주기적인 평균길이를 갖는 5개의 노란색 미끄럼자가 있습니다. 초기 단위체의 자들은 별 모양을 띠고 있습니다. 큰 파란색의 Q 준단위체는 좌상단에서 보이는 수레바퀴 체계의 파란 마름모와 관련이 있습니다. 여기서는 하나만의 자만이 표시되어 있고, 이는 빨간 쌍둥이 틀에 맞추며 유동적으로 움직일 수 있습니다. 자의 위치는 좌하단의 초기 단위체의 평행한 자에 의존합니다. 우측의 끝점 표시는 자의 위치를 평행한 회전고리에 연결되어 있는 우상단 검은 경계선 마름모의 초록색 틀에 옮길 수 있게 합니다. 그 위치는 좌상단 수레바퀴 체계의 초록 마름모와 관련되어 결정됩니다.
Q 준단위체의 세부모습
이 Q 준단위체의 세부모습에서, 아크릴 플렉시글라스 마름모의 위치는 이전 이미지의 것과 다릅니다. 하양 화살표는 마름모가 144° 회전한 방향을 말해줍니다. 하지만 이 두 자리 모두에서 Ammann 직선들을 연장할 수 있다는 것이 보장되기 때문에 둘 모두 짝짓기 규칙에 맞습니다.
이전 이미지에서 자의 우측 끝단 표시는 여기서는 보이지 않는 평행한 초록 틀의 자와 연결될 수 있습니다. 양끝점 모두가 노란 괄호로 표시된 평행 틀의 구간 속에 들어갈 수 있었기 때문입니다.
여기 보이는 마름모의 다른 위치에서는, 끝점이 노란 괄호로 표시된 공통 구간 밖에 존재합니다. 따라서 이 마름모 위치는 초기 단위체에 대해 상대적으로 혀옹되는 위치가 아닙니다. 준결정 연쇄 알고리즘(quasiperiodic succession algorithm)은 오로지 완벽한 수레바퀴 체계에 대응하는 위치만을 결정합니다. 수레바퀴 체계의 정의는 명확하고 무한합니다.
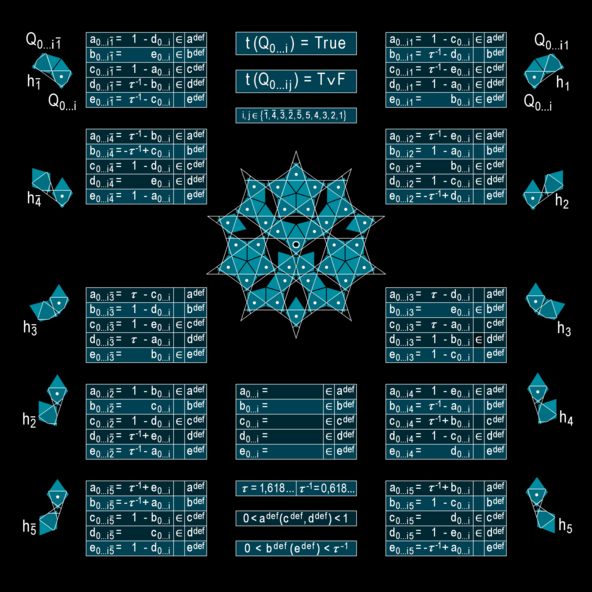
Algorithm of Decagonal Quasiperiodic Succession
The recursive formula consists of 50 scale value equations. The ten blocks in the outer columns correspond to the ten possible rhombus neighborhoods hj which are shown beside the columns. a, b, c, d and e are the values of the five double scales of a quasicell Q. The double scales are rotated by 36° to one another. Each thick rhombus can be assigned a quasicell Q.
The five values of the start cell Q0 are infinitesimally small, i. e. μ0 = 10^–n, with lim n → ∞. If they are entered in the central block, the formula leads to four valid neighbours, h1*, h2*, h4 and h1 (because their five respective values are valid) and six invalid neighbours (because one or more of their respective values are invalid). Please note that an asterisk is used here instead of an overline to indicate an inverse operation.
The valid values of Q01*, Q02*, Q04 and Q01are entered in the central block of four new formula sheets whereby the next generation of neighbours can be calculated. This recursiv scheme creates step by step an error-free quasiperiodic cartwheel order, as required for such a growth model.