Jean-Francois Colonna - Mathematics and Physics
물리학의 모습들
갈릴레오가 있었던 17세기로부터 2000년 혹은 그 이상 동안, 수학은 자연의 법칙들을 서술하는 언어로 생각되었습니다. 이는 현미경과 망원경 다음으로 우리 세계에 매일 새롭고 신비로운 관점을 보여주는 “관측기구”로서의 혁명이었습니다. 하지만 이 기구의 “극도의 효율성”(Eugene Wigner)의 원인과 그 본질은 더욱 신비롭게 보입니다. 가능한 설명은, 수학은 우리의 시공간 밖에 독립적으로 존재하며 현실 세계는 “그저” 이에 기반한 수학적 구조 중 하나이고, 의식적으로 행동하는 우리 또한 그 세부구조의 결과 중 하나라는 것입니다.
우리의 우주에 대한 이해를 넓히기 위해서는 수학이 필수적입니다. 공식을 조작하고 방정식을 푸는 이런 과정은 보통 추상적이지만, 진화가 우리에게 부여한 감각의 사용을 막지는 못합니다. 특히 우리의 시각은 항상 놀랄 준비가 되어 있고, 오늘날 컴퓨터의 발전은 새로운 실험적 접근인 가상현실을 가능하게 합니다. 이른바 가상실험은 특정 시스템의 가상 환경에서의 연구로 구성되어 있고, 그 범위는 기본입자에서 우주 전체까지 무엇이든 가능합니다. 상당한 계산 후에 얻은 원 결과 자체가 수많은 쓸모없는 수치값들에 그치지 않게 하기 위해서는 이들을 “연출하는” 과정이 필요합니다.
숫자에서 그림을 만들어내는 번역은 아이들의 색칠놀이와는 거리가 먼 작업입니다. 실제로는 우리가 다루는 수학적 대상들의 특징들은 간단하고 구체적인 표현을 쉽게 허용하지 않습니다. 따라서 이들의 모습은 자연스런 형상이 전혀 없고 (수들의 색은 무엇일까 하는 멍청한 질문들이 나타나게 되고) 보통 (상당히 높은) 고차원에 있을 뿐더러, (역학적인) 시간은 공간과 연결되어 있는 등등… 이 분야의 경험에 따르면 의도하건 의도하지 않건 있는 것을 숨기고 없는 것을 보여주는 과정이 매우 쉽게 일어납니다…
하지만 수학은 예술적 창조를 위한 도구이기도 합니다. 현대의 잠재적 예술의 개념을 생각한다면, 더 이상 그림이나 소리 뿐만이 아니라, 근본적인 수학적 모델 그 자체가 예술 작품이 될 것입니다. 근래의 Benoît Mandelbrot의 프랙탈 기하학의 발전에서도 그러하듯이, 발견의 길은 우리 앞에 끝없이 뻗어 있을 것입니다… 우리의 미래에 새 지평을 열어 줄 어떤 과학적, 예술적 놀라움이 우리를 기다릴까요?

Space-time at Planck scale
초끈이론은 우리에게 친근한 4차원 시간-공간 차원에서 7개의 추가적인 공간 차원을 추가합다. 이 7차원은 아주아주 작고(플랑크 길이) Calabi-Yau 다양체로 정의됩니다.

Calabi-Yau manifold
초끈이론은 우리에게 친근한 4차원 시간-공간 차원에서 7개의 추가적인 공간 차원을 추가합다. 이 7차원은 아주아주 작고(플랑크 길이) Calabi-Yau 다양체로 정의됩니다.

Quantum vacuum fluctuations
양자진공은 비어있지 않습니다. 어디서라도 끊임없이 입자들이 생성되고 소멸합니다(예를들어 전기양전자 쌍들). 이 사진은 아주 짧은 시간 동안의 양자진공 현상을 보여줍니다.
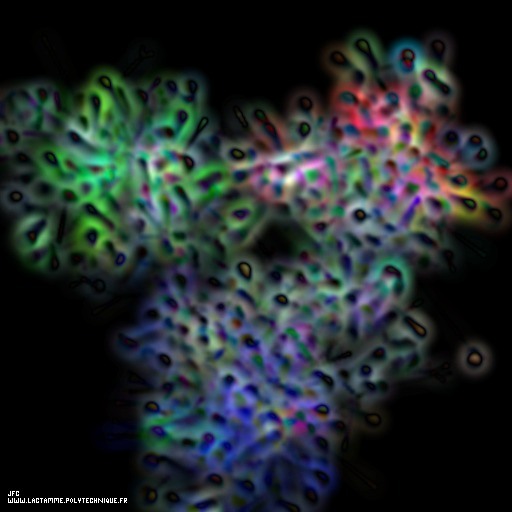
Quark and gluon structure of a nucleon
핵자(양성자 또는 중성자)는 기본 입자가 아닙니다. 그것은 쿼크들(작은 구형)과 강한 상호작용(강력)의 벡터들인 글루온들로 구성됩니다. 글루온의 “부피”는 서로 끊임없이 상호작용하는 가상 입자들로 가득 차 있습니다.


The Lorenz attractor
Lorenz attractor는 다음의 비선형 미분방정식들로 정의됩니다.
dx/dt=-10x + 10y
dy/dt=28x - y - xz
dz/dt=-8z/3 + xy
이 사진은 4차의 Runge-Kutta 방법을 사용하여 이 식들을 적분하여 얻은 것입니다.

Bidimensional visualization of the Verhulst dynamics
Verhulst 역학계는 다음의 반복으로 정의됩니다.
Xn+1=RXn(1-Xn)
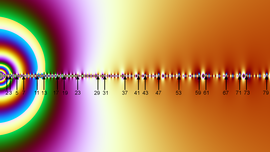
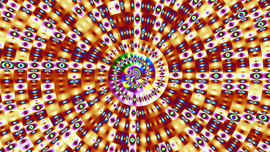
이 그림에서는 매개변수 R은 두 개의 값 R1과 R2 를 오갑니다. 이 두 값은 그림의 점의 X, Y좌표의 값으로 주어지고, 각각의 점이 나타내는 역학계의 Lyapunov 지수에 따라 색을 칠해서 얻어졌습니다. 회색, 주황, 빨강은 음의 지수를, 노랑, 초록, 파랑은 양의 지수를 나타냅니다.

Tridimensional visualization of the Verhulst dynamics
Verhulst 역학계는 다음의 반복으로 정의됩니다.
Xn+1=RXn(1-Xn)
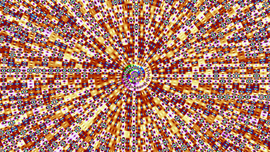
이 그림에서는 매개변수 R은 세 개의 값 R1, R2, R3를 오갑니다. 이 세 값은 그림의 점의 X, Y, Z좌표의 값으로 주어지고, 카오스 패턴이 나타나지 않는 역학계들에 점을 찍어서 만들어졌습니다.

Tridimensional brownian motion
(제목 번역: 3차원 브라운 운동)
점의 경로는 시간에 따라 자홍, 빨강, 노랑, 초록, 청록으로 색깔이 변합니다. 전체 모양의 2차원 그림자의 외부 경계가 하얀색 곡선으로 표시됩니다.
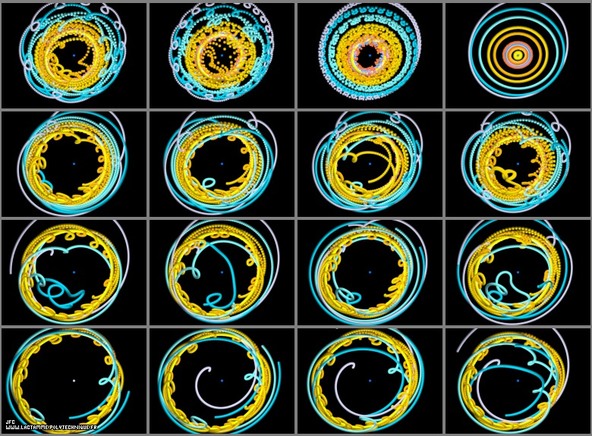
From the Sun to Pluto
오른쪽 상단의 사진은 태양중심의 태양계모형(해가 중심이다)을 보여주고, 왼쪽 하단의 사진은 이를 명왕성의 관점(명왕성이 중심)에서 보여줍니다. 14개의 남은 사진들은 태양에서 명왕성 사이의 중간 지점의 관점들을 보여줍니다.
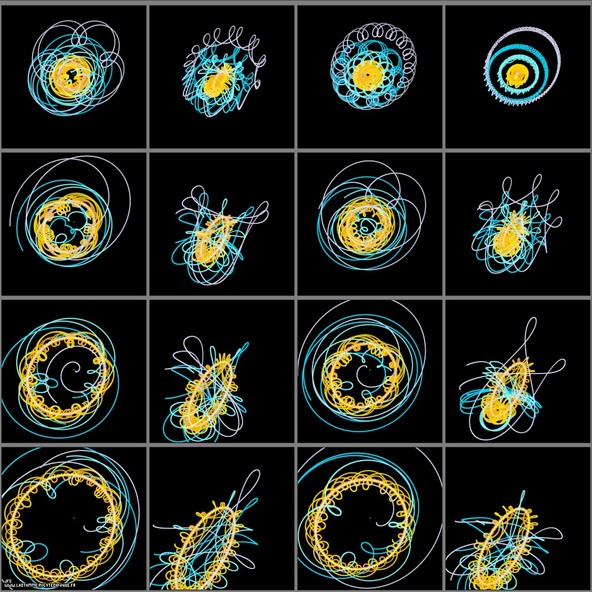
From the Sun to Pluto -extrapolation-
태양 중심의 태양계모형은 거의 완벽한 타원 궤도로 간단하게 나타납니다. 지구 중심의 태양계모형은 조금 더 복잡하고 프톨레마이오스의 주전원의 탄생을 가져왔습니다. 이 그림들은 태양보다 약간 멀리 황도면(ecliptic plane) 바깥에서 도는 16개의 다른 천체들에서의 관점을 보여줍니다.