Triangulating Unknown Environments using Robot Swarms
film
Licence
Credits
- Scientific Authors
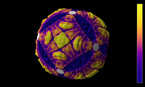
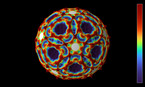
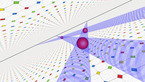
How can a robot swarm explore an unknown area and understand its layout? In this video, a swarm of R-one mobile robots is used for such a task. They are not trying to build an accurate floor plan, which requires expensive sensors. Instead, they sketch the area using a mathematical structure - a triangulation, which captures the essential topological features of the environment. This structure can be used to help other robots navigate through the area, and it can be created by low-cost robots with limited capabilities.
In recent years, the field of robotics has seen two diverging trends. One has been to achieve progress by increasing the capabilities of individual robots, keeping the cost of state-of-art machines relatively high. An opposite direction has been to develop simpler and cheaper platforms, at the expense of reducing the capabilities per robot. The latter raises new challenges for developing new principles and algorithms, such as coordinating many robots with limited capabilities into a swarm that can carry out difficult tasks, for example, exploration, surveillance, and guidance.
In this video, we show a recent collaboration between theory and practice of swarm robotics. We consider online problems related to exploring and surveying a region by a swarm of robots with limited communication range. The minimum relay triangulation problem (MRTP) asks for placing a minimum number of robots, such that their com- munication graph is a triangulated cover of the region. The maximum area triangulation problem (MATP) aims at finding a placement of n robots such that their communication graph contains a root and forms a triangulated cover of a maximum possible amount of area. We demonstrate the practical relevance of our methods by showing how they can be used on the novel real-world platform R-one.
This video belongs to the 22nd Annual Video and Multimedia Review of Computational Geometry, which is part of the 29th Annual Symposium on Computational Geometry.