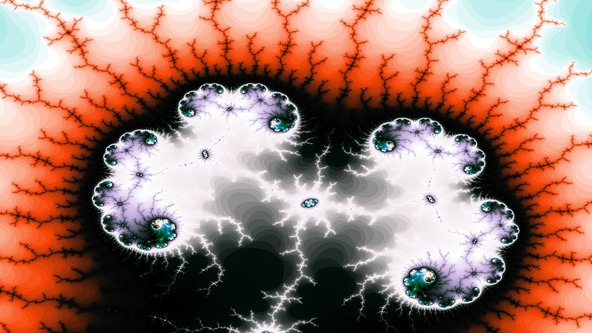
El conjunto de Mandelbrot de la familia cuadrática
Repetir una regla simple, una enorme cantidad de veces, puede parecer aburrido e inútil; por ejemplo, elevar un número al cuadrado. Si el número es grande, su cuadrado será mayor, y el cuadrado de su cuadrado será todavía más grande. Podemos decir que, en cada iteración, el resultado se acerca cada vez más al infinito. De hecho, esto le sucede a todos los números cuyo valor absoluto es mayor que uno. Por el contrario: si el número es pequeño, su cuadrado será menor, y con cada iteración sucesiva nos acercaremos arbitrariamente al cero. Las únicas excepciones de este comportamiento, entre los números reales, son el 0, el 1 y el -1.
Ahora bien, si la regla es un poco más complicada: elige un número: c, elévalo al cuadrado: c2 y toma la suma de ambos: c2 + c. De acuerdo a esta regla ¿cuáles números se van a infinito y cuales no?
Esta pregunta tiene una respuesta muy interesante si en lugar de considerar sólo a los números reales la extendemos a los números complejos; en particular porque los números complejos forman un plano, y en un plano podemos hacer dibujos.
El Conjunto de Mandelbrot de la familia cuadrática es precisamente el conjunto de números complejos que no escapan jamás a infinito, repitiendo infinitamente esta regla modificada.
En esta galería podrás observar al conjunto de Mandelbrot completo y algunos detalles de su forma.
Estas imágenes fueron generadas con el programa XaoS. Son acercamientos a detalles del conjunto de Mandelbrot que, de dibujarlo completo a esa escala, serían imagenes de tamaño entre el diámetro de la tierra (10-4) y hasta casi un año luz (10-14).