Matemáticas Visibles
Esta selección de imagenes es un subconjunto de la exposición ‘Matemáticas Visibles’ que se encuentra en los pasillos del Instituto de Matemáticas de la UNAM, en la ciudad de México, en la que colaboran varios artistas y matemáticos.
La curaduría de esta exposición estuvo a cargo de Aubin Arroyo, Julia Carrillo Escalera y Ana Retchman.
Esta selección de imagenes está diseñada para colocarse en mamparas de a lo más 90 x 70 cm. Están planeadas para colocarse en orden en una zona transitada por visitantes (el pasillo de una escuela, una institución o una plaza pública, por ejemplo) Son ocho imágenes y una portada y cada imágen viene acompañada de un texto informativo, en español, que trata de llamar la atención del observador hacia el área de las matemáticas en la que la imagen habita. El texto no asume ningun conocimiento matemático por parte del expectador.
Para obtener el material en alta resolución (para imprimir), descargue el archivo comprimido.
Nota: Las traducciones a otros idiomas son bienvenidas.


Superficies Algebraicas
Las ecuaciones son preguntas como estas: ¿cuál es el número -equis- que al restarle uno es igual a seis? o ¿cuál es el número -equis- que, al cuadrado, es igual a veinticinco? Cuando la pregunta es más complicada, escribir la ecuación con palabras agrega una complicación extra al problema de responderla.
Si bien la manera más simple de escribir la pregunta es usando la notación matemática en lugar de palabras: la letra equis, los exponentes y los signos de multiplicar, sumar y restar, esta notación tiene menos de 400 años que se utiliza.
En general, una ecuación en equis suele tener como respuesta apenas algunos pocos números. Sin embargo, si nos preguntamos por tres números a la vez, usando equis, ye y zeta, las repuestas son mucho más numerosas, al grado que, si las acomodamos todas en el espacio tridimensional, todas juntas forman una superficie y la forma de esta superficie está muy ligada con la ecuación.
La superficie en esta imagen es la respuesta a la ecuación x2-y(1-z2)2=0, que en palabras dice: ¿cuáles son los números equis, ye y zeta que, al elevar equis al cubo y restarle el resultado de multiplicar ye por el cuadrado de la diferencia entre uno y zeta cuadrada da cero?
Autor: Aubin Arroyo.
Área: Geometria Algebraica.

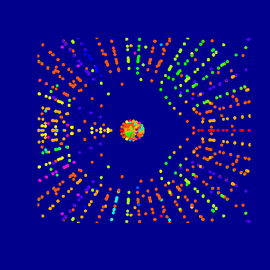
El Atractor de Lorenz
El Atractor de Lorenz se convirtió en el ejemplo del caos en matemáticas cuando empezaban a utilizar las computadoras para tratar de resolver algunas ecuaciones diferenciales, para predecir los fenómenos que evolucionan con el tiempo.
Las ecuaciones diferenciales también son preguntas, sin embargo la respuesta no es un número o una superficie. Resolver una ecuación diferencial significa, por ejemplo, encontrar una fórmula que permita calcular la posición de un satélite, seis meses después de haberlo colocado en órbita, o que permita calcular la temperatura, la humedad y la presión atmosférica en Acapulco, en las próximas vacaciones.
Si bien todas las ecuaciones tienen una solución exacta, algunas de estas se pueden calcular, por medio de aproximaciones con una computadora. Y, aunque no tengamos la posición exactísima de donde soltamos el satélite, los resultados que muestra la computadora nos servirán bastante bien por algunos años.
Sin embargo hay otras ecuaciones, como las que estudiaba el meteorólogo Edward N. Lorenz, que son muy sensibles: una pequeñísima diferencia en los números que usamos al calcular las aproximaciones nos pueden llevar a concluir resultados extremadamente diferentes: el caos.
Sin embargo, detrás de ese comportamiento aparentemente caótico, un conjunto con una estructura complicada, pero ordenada, determina el comportamiento de todas la soluciones de las ecuaciones de Lorenz. Este conjunto se llama El Atractor de Lorenz.
Autor: Aubin Arroyo.
Área: Sistemas Dinámicos, Ecuaciones Diferenciales.

Los dígitos de π
π = 3.14159265358979323…, el número ‘pi’, el que siempre resulta de dividir la longitud del perímetro de un círculo entre su diámetro; no importa de qué tamaño sea el círculo, y que se conoce desde la época de los egipcios, es un número que no es un quebrado entre dos números enteros. No se puede obtener como el resultado de dividir un entero entre otro. π es un número irracional.
Los decimales de los números irracionales no presentan ningún patrón periódico, que se repita indefinidamente; a diferencia de los racionales, o fracciones de números enteros, como el 1/3, que en decimales se escribe con una secuencia infinita de ‘3’: 0.333…
El número π tiene tantos decimales diferentes que puedes encontrar la fecha de tu nacimiento escrita en algún lugar de los dígitos. Una manera curiosa de representar los primeros 75 000 dígitos es este cuadro. El color de cada cuadrado de esta imagen está determinado por seis dígitos de π, dos para el rojo, dos para el verde y dos más para el azul, consecutivamente. El primero tiene 14% de rojo, 15% de verde y 92% de azul, y así sucesivamente.
Los matemáticos sospechan que, en algún lugar de los dígitos de π, codificados de esta manera, podemos encontrar la imagen de La Mona Lisa, de Da Vinci, o una foto del Castillo de Chapultepec, pero aún no lo confirman. Sin embargo, si están seguros de que esto pasa en este otro número:
0.1234567891011…
Autor: Aubin Arroyo.
Área: Teoría de los Números.

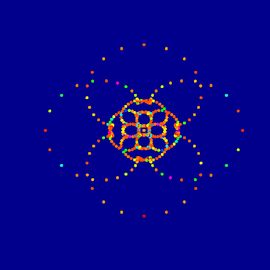
Las simetrías del cubo
Las simetrías, además de proporcionar un cierto confort a los sentidos del ser humano, son capaces de reconstruir a la forma en sí. Por ejemplo: El cubo es el poliedro regular delimitado por seis caras idénticas, cuadradas, pegadas por algunas de sus aristas, y que vive en el espacio tridimensional. El cubo es uno de los cinco sólidos Platónicos; y todos ellos son objetos extremadamente simétricos.
El cubo lo podemos girar por ciertos ejes, determinados ángulos, y obtenemos el mismo cubo, como si no hubiéramos hecho nada. También lo podemos reflejar con respecto a ciertos planos, sin alterar su forma. En total, el cubo tiene 48 simetrías. Sin embargo, todas estas simetrías las podemos representar con solo tres espejos colocados adecuadamente.
Esta imagen es una fotografía del interior del caleidoscopio Adhara hecho con cuatro espejos: tres de ellos codifican las simetrías del cubo y con el cuarto se produce una repetición infinita.
Título: Adhara.
Autor: Julia Carrillo Escalera.
Área: Geometría, Álgebra, Combinatoria.

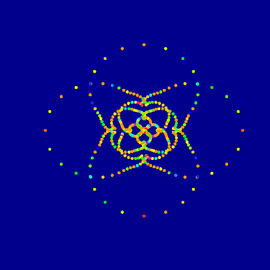
Hipercubo Quiral Mexicano
El hipercubo es pariente del cubo, pero que tiene una dimensión más: es un politopo y vive en el espacio de cuatro dimensiones. El hipercubo está formado por ocho cubos idénticos, pegados por algunas de sus caras que son cuadradas.
El cubo y el hipercubo comparten una propiedad que no muy sorprendente en sí misma. Su imagen reflejada en cualquier espejo es idéntica al original. Son más extrañas las formas que no tienen esta propiedad: las formas quirales.
Una mano derecha es diferente a una mano izquierda; cualquiera que haya intentado vestir el guante equivocado lo habrá comprobado. Sin embargo, la imagen en el espejo de una mano derecha es una mano izquierda y viceversa.
Por un buen tiempo se sospechó que no era posible que existieran politopos quirales en el espacio de cuatro dimensiones. Sin embargo, en el año 2012, un grupo de matemáticos mexicanos descubrieron al Hipercubo Quiral Mexicano que, a pesar de ser muy semejante al hipercubo, es distinto a su imagen en el espejo.
A pesar de que este objeto vive en la cuarta dimension, podemos hacernos una idea de como es, mediante sus proyecciones, o sombras. Esta imagen es una representación estilizada de una proyección del Hipercubo Quiral Mexicano.
Autores: Aubin Arroyo y Pedro Cerisola.
Área: Combinatoria.

Conjuntos Límite
Repetir obsesivamente una tarea sencilla y llevar esta repetición al límite puede traer resultados sorprendentes. Para los matemáticos, llevar una repetición al limite suele significar realizar dicha tarea sencilla no cien, ni cien mil veces, sino repetirla una infinidad de veces.
Reflejar en un espejo es, sin duda, una tarea sencilla, que por si sola no es sorprendente: lo que está de un lado del espejo se intercambia con lo que está del otro y viceversa. Sin embargo, si agregamos otro espejo, y observamos lo que sucede entre dos espejos paralelos, inmediatamente nos encontramos con una representación del infinito.
Si utilizamos varios espejos de forma esférica y los colocamos en los vértices de un cubo, por ejemplo, procurando que las esferas vecinas apenas se toquen, y observamos la repetición infinita de reflejos en todas las esferas, en el límite, encontraremos un conjunto fractal.
En esta imagen podemos observar el cuadro ‘Otras Revelaciones’ de Teresa Rubio reflejado en 40 esferas colocadas en un dodecaedro regular.
Autores: Aubin Arroyo y Teresa Rubio.
Área: Sistemas Dinámicos, Grupos Kleinianos.

Nudos Salvajes
Los nudos matemáticos se estudian en la topología y se clasifican en dos: los mansos y los salvajes. Los nudos mansos son los que se pueden construir con una cuerda en la vida real. Los nudos salvajes son los que no.
Anudar un collar es sencillo, pero si el collar está hecho de esferas y estas esferas son espejos, podemos observar un fenómeno parecido al que se produce al colocar dos espejos paralelos en una habitación. En cada una de las esferas del collar podríamos ver la imagen reflejada de las demás esferas, copiando el resto nudo. Y podríamos pensar que la imagen reflejada de todas las esferas forman un nuevo collar con esferas más pequeñas, adentro del collar original. Sin embargo, no hay razón para detenerse ahí. En cada una de las esferas de este nuevo collar sucede lo mismo: se refleja el resto del collar y en cada una de las imágenes reflejadas encontramos un pedazo de nudo cada vez más complicado.
En esta imagen podemos observar un pedazo de un nudo salvaje. Este está construido a partir de un collar, anudado, de esferas reflejantes; y en realidad, corresponde a la curva que está contenida en las sucesivas imágenes del collar en cada una de las esferas, iterativamente. Este curva tiene, además, naturaleza fractal.
Autor: Aubin Arroyo.
Área: Sistemas Dinámicos, Grupos Kleinianos, Teoría de Nudos.

Teselaciones Aperiódicas
Hay muchas y distintas maneras de recubrir el piso con mosaicos. Algunas utilizan piezas de distintas formas, tamaños y colores para elaborar imágenes reconocibles: un paisaje tropical o la figura de algún animal fantástico, por ejemplo. Otras maneras, con tan solo algunas pocas piezas diferentes, pero mediante patrones repetitivos, pueden cubrir el plano sin dejar ningún agujero descubierto. Con hexágonos regulares, todos del mismo tamaño, es posible recubrir el plano infinito por completo, como en un inmenso panal de abejas.
De manera abstracta, cuando la manera de colocar los mosaicos sigue un patrón periódico, este patrón debe ser alguno de los 17 patrones posibles llamados los 17 grupos cristalográficos del plano.
Sin embargo, hay maneras que, con algunas pocas piezas, se puede cubrir el plano infinito sin seguir ningún patrón. Estas son llamadas teselaciones aperiódicas. En esta imagen observamos una porción del plano cubierto con una de estas, llamada ‘la Teselación del Molinillo’.
Autor: Darío Alatorre.
Área: Combinatoria.