Circle Packing Explorations
There are several means of building set of tangent circles. One of them is called an Apollonian Gasket: it recursively fill the space between tangent circles. But this method leaves large empty spaces inside the initial circles. The idea is then to fill again those empty circles with the same algorithm, changing some parameters to induce some randomness and get some surprise at the end.
Another means is called the Steiner Chain: putting a chain of tangent circles between two circles.
Combining those two technics, with a little randomness, gives rise to an infinity of shapes.
This paper can help you going deeper into the subject:
http://www. lifl.fr/~decomite/papers/circlePacking.pdf
The programming part of the exploration is also part of the fun.

Circle Packing Exploration 1
This example also uses a Mobius transform, which slightly alter the circle disposition. Mobius transforms preserve circle and tangency between circle. There are then good tools to add some variations when generating the designs.
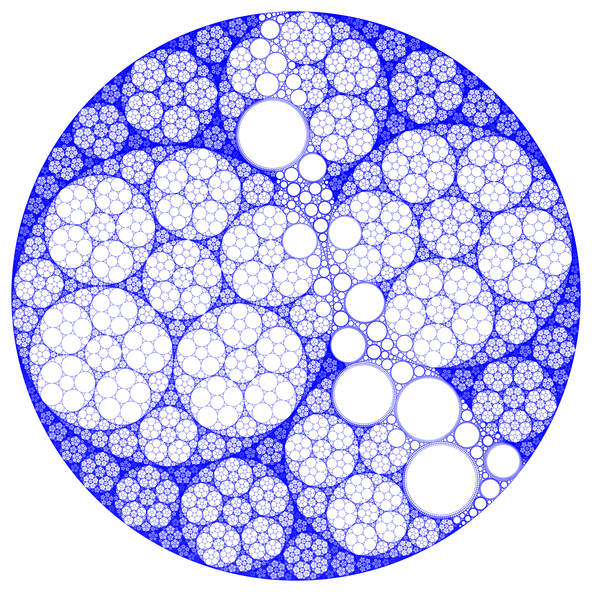
Recursive Apollonian Gasket
Not the best attempt, but this one might help understand the way the other images are build. Zoom into it to try to understand the algorithm.
A Whiter Shade of Deep Purple
here, a Mobius transform turned the universe upside down : the purple circles were initially very far from the center of the image. A nice way to create a camaieu in the center of the picture.

Devil's Hill
And when you are fed up with two-dimensional images, why not adding a third one ? Circles are replaced with cylinders whose height is computed with a gauss function.

A catalog of circle packing tries
This catalog only shows a little part of which structures we can generate with very few parameters





















