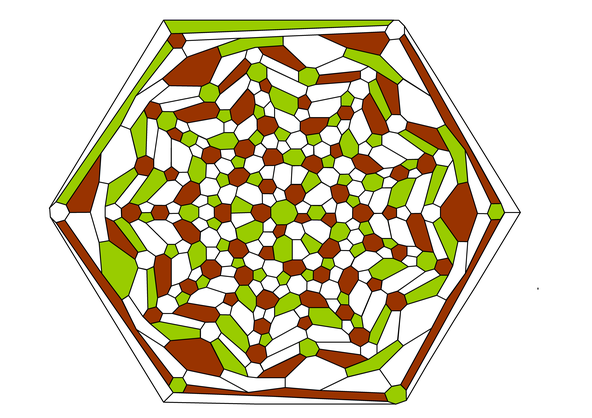
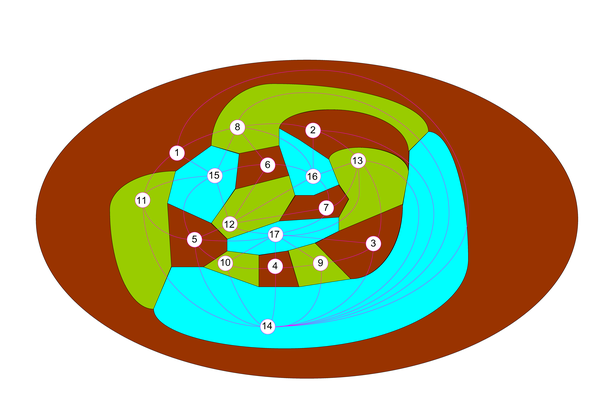
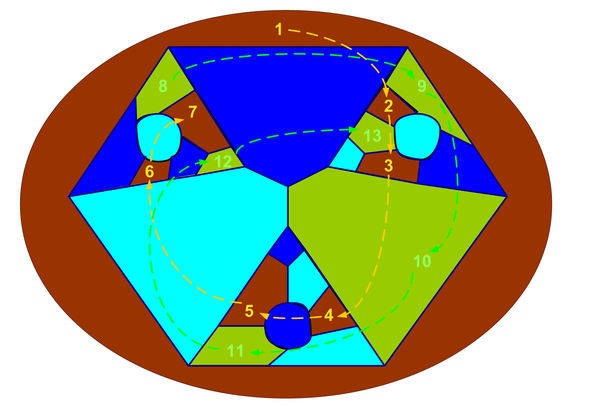
Create your own four-colored world
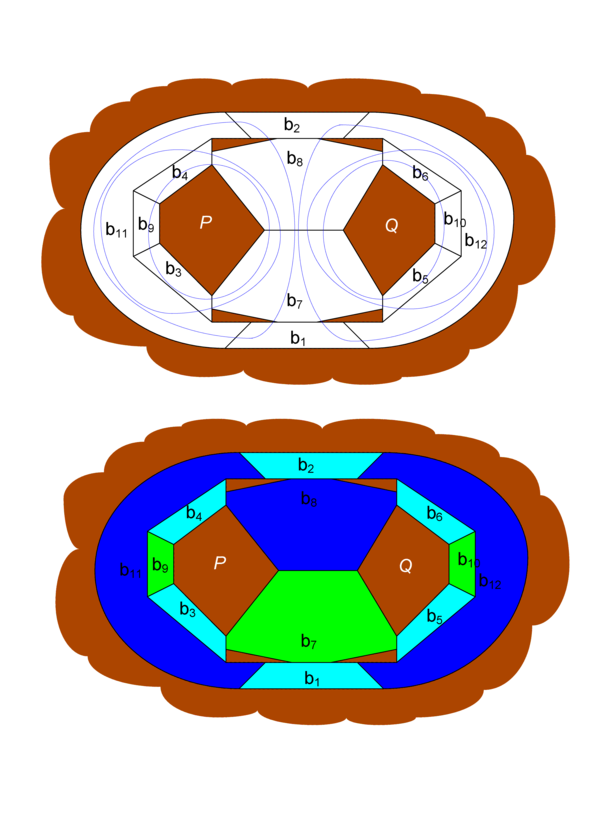
Our algorithmic method has been given in three steps. The first two steps are the maximal mono-chromatic and then maximal di-chromatic coloring of the faces in such a way that the resulting uncolored (white) regions of the incomplete two-colored map induce no odd-cycles so that in the (final) third step four coloring of the map has been obtained almost trivially. In order to make the map-coloring algorithm more visible and meaningful let us define the four-color set as
C = {B,G, dB, lB}, where
- B denotes brown color and when it is assigned on to the white background color the corresponding region becomes a “high-land”.
- G denotes green color and when it is assigned on to the white background color the corresponding region becomes a “low-land”.
- dB denotes dark-blue color and when it is assigned on to the white background color the corresponding region becomes a “deep sea”.
- lB denotes light-blue color and when it is assigned on to the white background color the corresponding region becomes a “shallow-sea”.
Initially the given map colored all by background color white and at the end of the coloring algorithm (three steps) it will be colored by the colors C and no white color remains on the map.
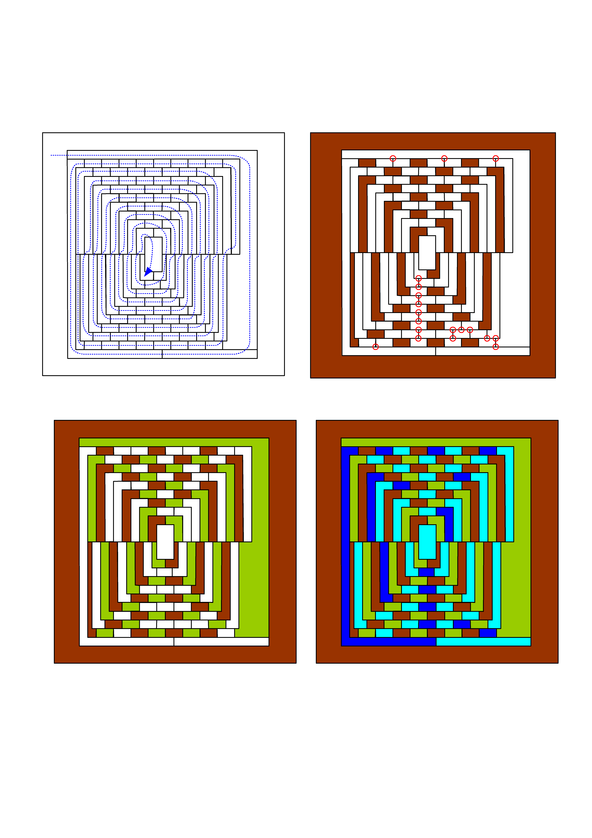
Maximal mono-chromatic coloring of the Appel and Haken's map
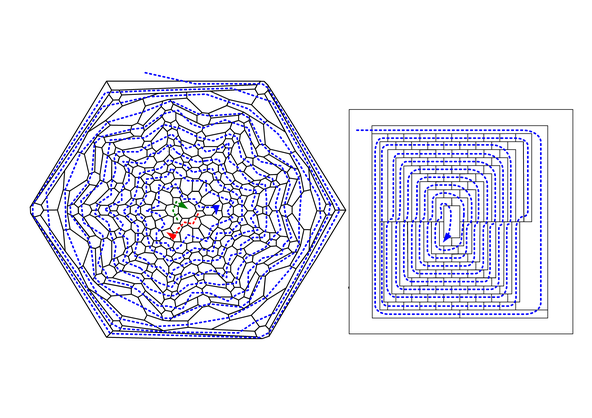
Maximal mono-chromatic coloring of high-land (brown) regions. Note that we start coloring from the outer region and must be all adjacent to white (not colored) regions. Intersection of three adjacent regions have been shown with small circles (unwanted spots) and must be vanished as shown in the maximal 2-coloring of the map.
Maximal di-chromatic coloring of the Appel and Haken's map
Maximal two coloring of high-land (brown) and low-land (green) regions. Green coloring starts from the upper white region (can be started from any white region adjacent to outer region). Trace of green regions form a spiraling in the clockwise direction and at each step at least one “circle” of the previous figure is vanished by the assignment of the green color to a white region.
Four coloring of Appel and Haken’s map
Final four coloring of Appel and Haken’s map; The white regions of the maximal di-chromatic map colored by the two colors of deep sea (dark blue) and shallow sea (light blue).
When three colors is enough
The three colored map M is an illustration of Heawood’s theorem: A normal map M is 3-colorable if and only if its dual planar graph G has an even triangulation. In the figure three coloring of M is obtained by the Map Coloring Algorithm. Numbers assigned shows the spiral order of the regions in the coloring e. g.,
1,2,3,4,5,6,7 (Step 1 for high-lands),
8,9,10,11,12,13 (Step 2 for low-lands),
14,15,16,17 (Step 3 for shallow-seas).
Here we may call the shallow seas as lakes since they all surrounded by land regions.
Martin Gardner's Map
Martin Gardner’s April Fool’s joke (1975). (a) The “counterexample”
map, (b) Brown highland islands, (c) Brown-green high-low islands
and (d) The four colored map. Note that (i) each color spiraling in the map and (ii) white regions in (c) induced disjoint union of acyclic subgraphs.
Double spiral chain coloring of Martin Gardner's map
In the figure we have shown strong four coloring of the Martin Gardner’s map by the use of double spiral chain ordering
and coloring e. g., one of the spiral leg is the (Green,Brown)-Kempe chain while the other (Light-blue,Dark-blue)-Kempe chain. We suspect that if the given map is hamiltonian then double-spiral ordering results in strong four coloring of the map.
Tutte's graph as seen normal map
This is the famous Tutte’s graph (1946) which disproves Tait’s
conjecture that every 3-regular 3-edge-connected planar graph is hamiltonian. When the Tutte’s graph as seen cubic planar map (normal map) is an example of non-existence of a strong four coloring. In fact in 1971 Stein observed that a normal map has strong 4-coloring or B-set iff its associated cubic graph is hamiltonian. However as shown above spiral ordering with the map coloring algorithm results a 4-colored map.
Spiraling of the Haken and Appel’s and Martin Gardner’s maps
You may need more than one spirals to cover the regions of the map (see the map on the left).
Fake counter-example
Spiral ordering of the regions for this map results strong four coloring e. g., decomposes into two Kempe chains, hence showing that it is also Hamiltonian (see the boundaries in bold-lines in the map (right)).
Blocking white odd-cycles
After the maximal mono-chromatic coloring of the map we have to remove all white odd cycle in the maximal dichromatic coloring. Here color green of the regions b_9 and b_10 removes the spots (cycles of lenght three) and color green of region b_7 blocks all of the odd-cycles.
