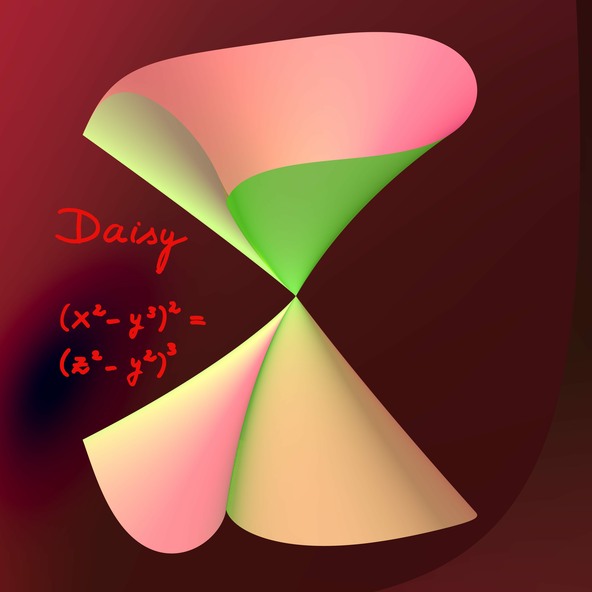The Italian premiere of a large IMAGINARY exhibition
Herwig Hauser Classic
Les surfaces algébriques classiques d’Herwig Hauser sont compilées pour l’exposition IMAGINARY originale. Les formes et les formules d’Herwig Hauser sont choisies de sorte à ce que les équations soient simples et élégantes. Les figures sont claires et naturelles et montrent des propriétés géométriques remarquables. Herwig Hauser est professeur de mathématiques à l’Université de Vienne et travaille en géométrie algébrique et en théorie des singularités.
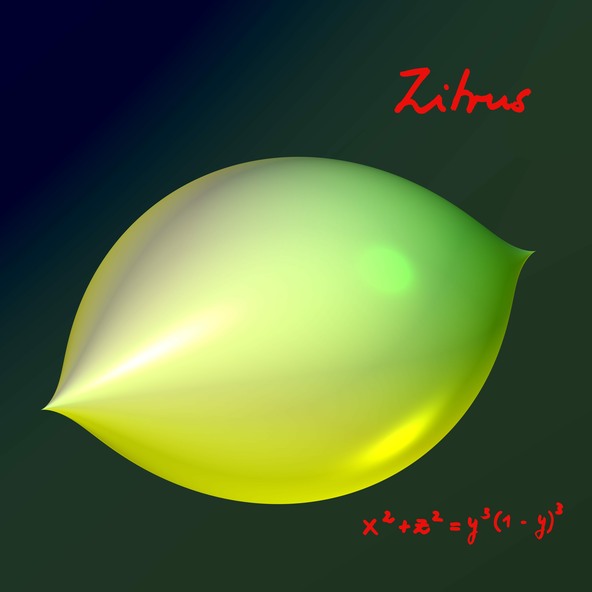
Zitrus (Agrume)
L’équation x2+z2 = y3(1−y)3 d’Agrume (Zitrus) semble aussi simple que la figure elle-même. Deux pointes symétriques l’une de l’autre par réflexion tournent autour d’un axe traversant. L’équation simplifiée x2+z2 = y3 en omettant (1−y)3 ou inversement fournissent deux images-miroir. Toutes deux sont des surfaces d’extension infinie. Le produit des deux termes de droite de l’équation initiale assure que Zitrus reste bornée. On peut se représenter ceci en remarquant que si la valeur absolue de y devient plus grande que 1, alors le membre de droite devient négatif et l’équation n’admet pas de solution réelle pour x et z.
Limão (Citron)
Cette surface d’équation x2 = y3z3 est difficile à visualiser de manière attrayante. L’éclairage et la forme posent tous deux problème près de l’origine, du fait que l’image doive présenter la figure de manière la plus authentique possible. Cela tient à la géométrie et surtout à l’angle de la prise de vue.
Des artefacts se produisent ici et là, tels que des effilochages ou des marbrures, sans pour autant correspondre à une réalité mathématique. De même, les réflexions peuvent produire un effet perturbant. Le long des arêtes, du flou apparaît près du bord malgré la qualité du programme POVRay. Le problème se situe en fait au niveau de la complexité à résoudre les équations près des singularités. La soi-disante résolution des singularités, en donnant une paramétrisation de la surface, peut aider dans de nombreux cas.
Vis à Vis
Ici, deux phénomènes fondamentaux de la géométrie algébrique se font face. Le pic de la singularité de gauche dévisage une colline courbée mais lisse sur la droite. Cette deuxième singularité est en fait plus attrayante, car des modifications diverses de l‘équation entraînent des changements imprévisibles dans la figure, ce qui n‘arrive pas à des points “normaux”. En utilisant le programme SURFER, de telles surfaces peuvent être engendrées et modifiées d‘une manière simple et intuitive. La comparaison de la formule et de sa forme associée, c‘est-à-dire de l‘équation et de sa surface, devient une expérience interactive intrigante et intéressante.
Calypso
La surface Calypso d’équation x2+y2z = z2 contient trois droites. La droite horizontale est clairement visible, elle passe par l’origine (zéro) où la partie haute et la partie basse se rencontrent. Les deux autres droites se trouvent dans un plan vertical et elles se coupent au point 0. L’intersection de la surface et de ce plan fait apparaître ces deux droites.
Si l’on déplace ce plan légèrement vers l’avant, la courbe d’intersection devient une hyperbole. Ceci peut être facilement vérifié par un calcul. On pose soit y=0, soit y=1. Dans le premier cas, le résultat est x2 = z2 ou encore (x−z)(x + z) = 0, équation de deux droites dans le plan. Dans le deuxième cas, on obtient x2+z = z2. Cela peut se réécrire comme −x2+(z−1/2)2 = 1/4, équation d’une hyperbole centrée en (0, 1/2).
Calyx
La surface Calyx d’équation x2+y2z3 = z4 a comme lieu de singularités une droite. La partie basse de la surface a des singularités en pointe cachées le long de la droite, tandis que la partie haute rencontre cette droite tangentiellement en un point, l’origine. L’image réelle est trompeuse du fait que le polynôme définissant est irréductible et la surface, par conséquent, n’a qu’une seule composante algébrique (et non deux composantes comme semble le suggérer la figure).
On peut montrer que Calyx s’obtient comme une certaine projection de Calypso. Dans l’espace à trois dimensions, une surface cylindrique est contractée en la droite singulière de Calyx. Algébriquement, cette application est définie par la donnée très simple (x, y, z) → (xz, y, z). La substitution dans x2+y2z3 = z4 puis la réduction de z2 permet d’obtenir l’équation de Calypso x2+y2z = z2.
Daisy
L’équation (x2−y3)2 = (z2−y2)3 de Daisy implique par différentiation que le lieu des singularités est formé par deux courbes (planes) qui s’intersectent transversalement en leur point singulier commun. Afin de mieux comprendre les singularités, le géomètre construit leurs résolutions au moyen d’éclatements. En un nombre fini d’étapes, elles fournissent une surface sans singularité (une variété lisse) avec une application de projection sur la surface initiale qui s’interprète alors comme l‹ «ombre» de la variété.
Diabolo
L’équation du Diabolo x2 = (y2+z2)2 se factorise en le produit (x−y2−z2)(x+y2+z2) = 0. Ainsi, la surface est la réunion de deux paraboloïdes de révolution x = ±(y2+z2). Ils se touchent tangentiellement à l’origine. Le contact est algébriquement décrit par le terme linéaire x dans les deux facteurs. Le plan tangent est le plan vertical x=0.
Les bandes de couleur de l’image sont des ombres dues à l’éclairage. Si l’on modifie l’équation du Diabolo en ajoutant un terme constant comme dans x2 = (y2+z2)2+1/1000, alors les deux moitiés sont séparées. Cependant, en substituant x+y à x, on obtient la variante (x+y)2 = (y2+z2)2 de l’équation. Les deux coquilles sont déplacées d’un angle l’une de l’autre.
Ding Dong
Cette surface décrite par l’équation x²+y²+z³ = z² fut l’une des toutes premières visualisations que nous avons essayées. L’équation et la forme sont simples : une boucle verticale en forme d’alpha tourne autour de l’axe z. Mais il y eut un problème avec la coloration. Le vert est généralement assez compliqué pour les visualisations tridimensionnelles de surfaces et a de plus tendance à devenir mat ou à jaunir. L’éclairage et la réflexion doivent être bien testés. Notons que l’ombre en disque bleu clair intensifie l’effet d’espace.

Formule
- x^2+y^2+z^2+1500\cdot(x^2+y^2)\cdot(x^2+z^2)\cdot(y^2+z^2)-1=0
Distel (Chardon)
La surface Distel (Chardon) d’équation x2+y2+z2+c(x2+y2)(x2+z2)(y2+z2) = 1 est remarquable par son extraordinaire symétrie. L’image réelle a été obtenue avec une valeur très grande du coefficient c. Les six pics sont situés sur les trois axes de coordonnées de l’espace euclidien. Toute transformation permutant les trois axes laisse le Chardon inchangé. Le groupe des symétries est par conséquent celui du cube et de son dual, l’octaèdre, qui constituent deux des cinq solides platoniciens.
Curieusement, il n’est pas possible de construire des étoiles totalement régulières comme ce Chardon ayant n’importe quel nombre donné de pics. Il ne peut y avoir que quatre, six, huit, douze ou vingt pics, suivant les nombres de faces respectifs des solides platoniciens. Le lecteur curieux pourra tenter de trouver lui-même les équations pour chacune de ces étoiles.
Dullo
Si des supporters de football dans un stade circulaire s’époumonent quand leur équipe marque un but, le son qu’ils produisent s’étend comme un anneau qui gonflerait autour d’eux. Après une seconde ou deux, toute la surface est balayée par le son, et cet anneau s’intersecte lui-même au centre du stade. Des ondes sonores provenant de tous les points s’y concentrent. On peut imaginer que c’est une des raisons pour lesquelles les arbitres suivent la balle: s’ils restaient au centre du stade ils risqueraient la surdité.
Eistüte (Cône)
La section horizontale de ce cône est une courbe de rosette. Une petite roue tourne à l‘intérieur d‘un anneau, tandis qu‘une pointe placée sur la roue trace une courbe (comme dans un spirographe).
Différentes courbes sont produites, dépendant du rapport des deux rayons. Cette courbe se referme si ce rapport est rationnel.
Dans notre cas, c’est un trèfle à quatre feuilles. Notre cône, contrairement à ceux disponibles dans le commerce, permet à quatre boules de glace de tenir dans le cornet !
Helix
La lemniscate est la courbe plane d’équation y4+z2 = y2. Elle se déduit du cercle y2+z2 =1 en substituant z/y à z. Géométriquement, cette substitution correspond à la déformation d’un cercle en une boucle en «huit». En considérant y4+z2 = y2 comme une équation en les trois variables x, y et z, l’ensemble des solutions est une surface de l’espace de dimension trois, en fait un cylindre s’appuyant sur la lemniscate.
L’équation de Helix y4+x2z2 = y2 est obtenue par la substitution de xz à z. D’un point de vue géométrique, cette construction est une sorte de pliage. La symétrie par rapport à x et z est bien visible. Afin d’étirer légèrement Helix, les facteurs 2 et 6 ont été rajoutés. Le lieu singulier est l’intersection des droites. Les intersections de Helix avec les plans x = c ou z = c sont des lemniscates si c ≠ 0, tandis que les intersections y = c sont des paires d’hyperboles.
Herz (Cœur)
Malgré la simplicité de son équation y2+z3 = z4+x2z2, la surface Herz (Cœur) possède une structure locale et globale subtile. L’ensemble singulier est une droite sur laquelle la surface s’intersecte elle-même. Le point origine 0 est remarquable car de l’intersection du Cœur avec un plan x = c orthogonal à la droite singulière est une boucle qui se serre comme un noeud lorsque c tend vers 0. Un entonnoir se forme.
De loin, on aperçoit une ouverture circulaire sur la surface. L’intersection avec le plan xy vertical est bien un cercle. La simplicité de la surface nous permet de fermer les yeux tout en se remémorant en détail la figure. Il est cependant bien plus difficile de décrire oralement la structure géométrique par manque de termes courants adaptés.
Himmel & Hölle (Paradis et Enfer)
Un morceau de papier est plié et tenu de telle manière que vous puissiez mettre vos doigts dans les quatre coins ainsi formés. En écartant les doigts, la figure s‘ouvre de deux manières différentes, si bien que deux des quatre bords intérieurs peuvent être vus en même temps.
Cette figure nous rappelle le jeu de cour de récréation où on doit tirer une couleur et déplier un coin pour connaître son avenir, bleu pour le ciel et rouge pour l‘enfer, d‘où son nom.
En ajoutant les exposants des carrés en y et z, on obtient le plus haut exposant: 4. C‘est une équation du 4ème degré. Plus le degré est élevé, plus la surface est difficile à calculer.
Kolibri (Colibri)
Vous avez peut-être remarqué que le Colibri est une vue rapprochée et renversée de Herz (Cœur) près de l’origine. L’équation x3+x2z2 = y2 est à comparer avec celle de Herz y2+z3 = z4+x2z2. Il est possible de transformer l’une en l’autre par un changement de coordonnées.
Le colibri est l’un des plus petits oiseaux et est doté de facultés impressionnantes. Ses ailes peuvent battre jusqu’à 200 fois par seconde afin qu’il puisse voler sur place en l’air. Cette activité demande beaucoup d’énergie, c’est pourquoi le Colibri doit ingérer deux fois son poids en nourriture chaque jour. En l’absence d’une source de nourriture constante, il mourrait de faim en quelques heures. Sa température corporelle diminue considérablement pendant la nuit afin d’économiser son l’énergie.
Kreisel (Toupie)
Il faut des mathématiques inventives pour décrire la forme du Kreisel (Toupie) comme solution d’une équation algébrique simple ! À première vue, il n’est en effet pas mathématiquement évident de dire à quoi doit ressembler l’équation, car d’autres équations peuvent produire des surfaces ressemblantes.
L’image illustre l’équation 60(x2+y2)z4 = (60−x2−y2−z2)3. La symétrie de révolution autour de l’axe vertical z provient du fait que x et y apparaissent toujours sous la forme du polynôme x2+y2. La puissance troisième dans le membre de droite est nécessaire pour créer les deux pointes. Ensuite, l’apparition de z uniquement à des puissances paires entraîne que la surface est symétrique par rapport au plan horizontal xy. Le paramètre 60 dans l’équation est introduit pour des raisons esthétiques.
Miau
Cette surface est apparue, par hasard, pendant un ennuyeux voyage en train (la visualisation de surfaces algébriques fait paraître le temps moins long pendant les voyages en train ennuyeux!).
Deviner son équation algébrique s’est avéré difficile, en particulier pour obtenir l‘ouverture double avec sa singularité.
Pour certains mathématiciens, explorer la relation entre l‘équation et la forme est un délicieux passe-temps, un coffre aux trésors où l‘on découvre des merveilles.
Nepali
Observons l’équation définissante (xy−z3−1)2 = (1−x2−y2)3de Nepali. La symétrie entre x et y résulte du polynôme quadratique x2+y2, qui est symétrique de révolution à la différence du monôme xy. L’intersection par les plans horizontaux z = c produit des courbes fermées qui sont presque des cercles. L’occurrence simultanée des puissances deux et trois engendre un rétrécissement en haut.
La courbe formée par le bord latéral de Nepali n’est pas exactement un cercle mais monte et descend tel le bord d’un chapeau. Sa projection sur le plan horizontal xy est tout de même un cercle, tel qu’il peut être vu depuis le haut. La surface est bornée; il n’y a donc pas besoin de tronquer la vue au moyen d’une intersection avec une sphère. Ce fait peut être établi par une analyse précise de la formule.
Seepferdchen (Hippocampe)
Si vous voulez deviner l‘équation de cette surface, vous aurez besoin de travail, de chance et de courage! Le contact tangentiel n‘est pas facile à obtenir car il disparaît au moindre changement de la formule.
L‘élégance de l‘Hippocampe est une illusion car vu de l‘autre côté il n‘est pas aussi beau. Les hippocampes vivent dans les zones climatiques tropicales et tempérées. Leur nom latin est Hippocampus et leur équation figure ci-dessus.
Solitude
L’équation x2yz+xy2+y3+y3z = x2z2 de Solitude n’est pas révélatrice de sa diversité géométrique cachée. De même, l’image ne montre qu’une partie des caractéristiques. Ce qui est en revanche plus éclairant est la rotation de la caméra telle qu’on peut la voir dans le film «ZEROSET - I spy with my little eye».
Il y a deux ouvertures évidentes, la première bien visible et une autre plus petite, que l’on ne soupçonnerait pas au premier abord. La vue de dessus montre la droite singulière verticale le long de laquelle les sections horizontales sont des courbes avec une pointe. L’exemple de Solitude illustre la complexité de déduire la géométrie visible à partir de l’équation. De même, on peut explorer les aspects complexes ou de théorie des nombres de la géométrie sous-jacente.
Tanz (Danse)
En posant z = 0 dans l’équation 2x4 = x2 +y2z2 de Tanz (Danse), on obtient l’équation 2x4 = x2. Celle-ci décrit l’intersection de Danse avec le plan horizontal xy. En réécrivant l’équation, vous obtiendrez x2(√2x+1) (√2x−1) = 0, équation de trois droites parallèles. On peut observer ici un phénomène typique de géométrie réelle: la droite x = z = 0 est incluse dans l’ensemble des solutions de l’équation de Danse 2x4 = x2+y2z2, mais en est une composante isolée unidimensionnelle. En effet, pour x proche de 0, il n’y a pour seules solutions que les solutions de x = y = 0 ou x = z = 0, c’est-à-dire la croix constituée des axes y et z.
Les droites étant infiniment fines, elles ne sont pas prises en compte par le programme de visualisation, ou ne sont pas indiquées. L’existence des composantes unidimensionnelles de l’ensemble des solutions doit donc être établie par un calcul préalable avant qu’elles soient ajoutées à l’image sous la forme de fins cylindres si nécessaire.
Taube (Colombe)
La Colombe (Taube) possède l’étonnante formule:
256z3 − 128x2z2+16x4z+144xy2z−4x3y2−27y4 = 0.
Les coefficients ne sont pas choisis au hasard. Au contraire, l’équation provient d’une autre formule plus générale, connue sous le nom de discriminant. Il décrit l’ombre d’une surface ou d’une variété, obtenue par la projection de celle-ci sur une surface ou sur un espace vectoriel de plus grande dimension. La trace obtenue est clairement définie par la surface et par la projection, de même que la forme de l’équation d’un point de vue algébrique.
Tülle (Bec verseur)
La surface Tülle (Bec verseur) est l’union de trois composantes régulières qui s’intersectent deux à deux en une courbe plane toute aussi régulière. Trois courbes d’intersection sont ainsi obtenues: une droite et deux paraboles qui se rencontrent tangentiellement à l’origine. Nous avons ici l’exemple le plus simple d’une surface avec trois composantes deux à deux tranverses telle que les courbes d’intersection entre les différentes paires de composantes se coupent de manière non-tranverse. La surface n’est donc pas la variété Mikado.
L’intersection transverse de deux composantes régulières d’une surface - un concept fondamental en géométrie - peut, au moyen de la théorie dite des idéaux, être mise en équation de manière algébrique et précise. On peut alors l’utiliser pour des calculs et des démonstrations. Dans le cas de composantes singulières, une définition correcte de la transversalité se fait toujours attendre.
Zeck (Tique)
L’équation simple du Tique (Zeck) x2+y2 = z3(1−z) dicte complètement sa géométrie de même que pour les autres surfaces; cela signifie que les points singuliers, la forme globale, la courbure et l’extension sont clairement définis par les quatre monômes x2, y2, −z3 et z4. Par conséquent, la formule est un moyen très efficace de coder les formes d’apparence complexe. Toutefois, l’information géométrique n’est pas toujours lisible sur la formule. La forme locale de la surface au voisinage d’un point donné peut être décrite explicitement dans la plupart des cas; les techniques de géométrie analytique locale sont ici efficaces. La description de la structure globale demande en revanche bien plus de travail et ne peut pas toujours être réalisée de manière satisfaisante.