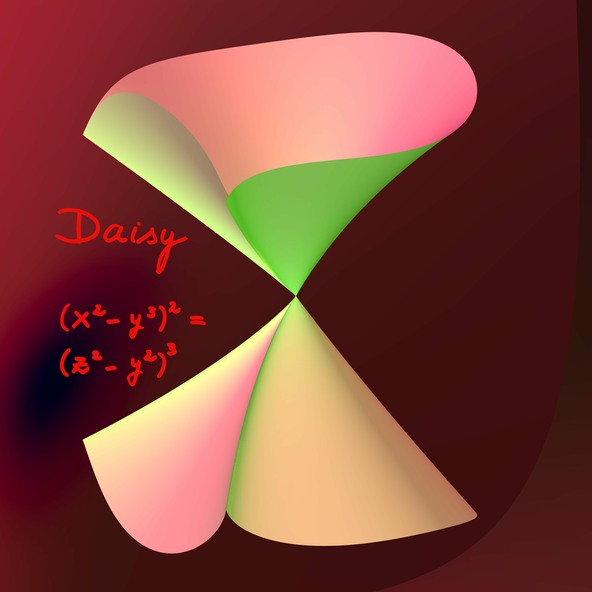Matematik eğlencelidir! 6 Haziran saat 11:00›de iki yeni etkileşimli istasyon EXPERIMINTA Bilim Merkezi’nde (Frankfurt, Almanya) sergilenecek. Açılışa Goethe Üniversitesi’nden Prof. Oldenburg ve Oberwolfach Matematik Araştırma Enstitüsü’nden Dr. Matt katılacak. Muheteşem görsellerle dolu bu iki istasyon, daimi olarak bilim merkezinde sergilenmeye devam edecek.
Klasik Herwig Hauser Yüzeyleri
Herwig Hauser’in klasik cebirsel yüzeyleri IMAGINARY sergisi için derlenmiştir. Bu yüzeyler en basit ve güzel denklemlere sahip olacak şekilde seçilmiştir. Gayet sade ve doğal olan görseller ilginç geometrik gerçekleri gözler önüne seriyor. Herwig Hauser Viyana Üniversitesi Matematik bölümünde cebirsel geometri ve tekillik teorisi alanlarında çalışan bir profesördür.
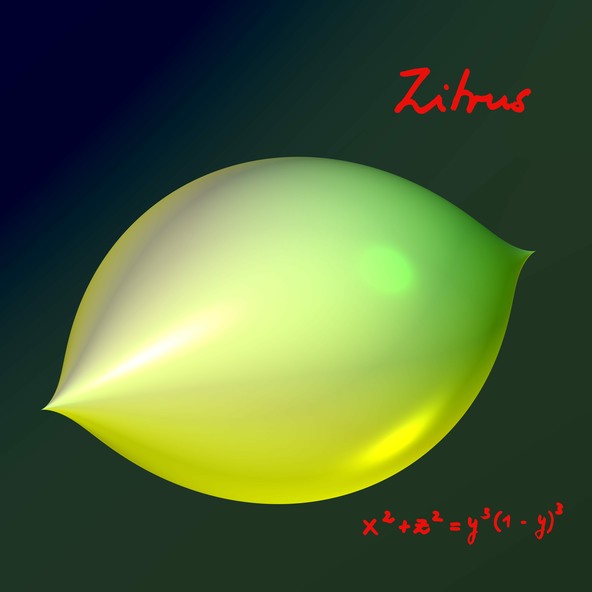
Limon
Bu limonun denklemi x²+z² = y³(1-y)³… Şekli kadar basit görünüyor. Karşılıklı olarak yerleştirilmiş iki sivri uç nokta (gaga) o noktalardan geçen eksen etrafında döndürülür. (1-y)³ çarpanını yok sayarsak, basitleşen x²+z² = y³ denklemi o gagalardan bir tanesini verir. x²+z² = (1-y)³ ise aynı şeklin ayna simetrisini verir. Bunların ikisi de sonsuza kadar devam eden yüzeylerdir. Asıl limonun sınırlı olarak kalmasını sağlayan, denklemin sağ tarafındaki çarpımdır. Şu şekilde düşünebilirsiniz: eğer y’nin mutlak değeri 1’den büyükse sağ taraf negatif olur ve denklemin x ve z için gerçek (reel) çözümü olmaz.
Limão
This surface with the equation x2 = y3z3 is difficult to visualize in an appealing manner. Both the lighting and the shaping near the origin produce problems, since the image shall present the figure as authentically as possible. This depends on the geometry and above all on the viewing angle of the camera. Artifacts occur, now and again, such as frayings or mottled colourings, which do not correspond to mathematical reality. Also, reflections can have a disturbing effect. Alongside the edges, mist is coming up near the intercept point, despite the quality of the POVRay program. The problem rather lies in the complexity to solve equations near singular points. The so-called resolution of singularities, which provides a parametrization of the surface, can help in many cases.
Vis á Vis
Vis à Vis means opposite – and, here, two essential phenomena of algebraic geometry stand opposite each other. The singular tip on the left looks at a curved but smooth hill on the right. This singularity is more exciting, because various changes to the equation can result in unpredictable changes to the figure, which does not happen at smooth points. By using the SURFER program, such surfaces can be generated and modified quite easily and intuitively. The comparison of form and formula, i. e. of equation and corresponding surface, becomes an interactive experience which is intriguing to understand.
Calypso
The surface Calypso with equation x2+y2z = z2 contains three straight lines. The horizontal straight line is clearly visible, it passes through the origin (zero) where the upper and lower part meet. The two other straight lines lie in a vertical plane, they also pass through 0 and intersect each other at that point. The section of the surface with this plane shows the two straight lines.
If you shift this plane a bit forward the section curve turns into a hyperbola. This can be easily checked by calculation. You set either y=0 or y=1. In the first case the result is x2 = z2 or (x−z)(x + z) = 0, the equation of two straight lines in the plane. In the second case you get x2+z = z2. This can be rewritten in −x2+(z−1/2)2 = 1/4, the equation of a hyperbola with centre at (0, 1/2).
Calyx
The surface Calyx with equation x2+y2z3 = z4 has a straight line as its singular locus. The lower part of the surface has cusp-shaped singularities alongside the straight line, whereas the upper part tangentially touches the straight line at a point, the origin. The real image is misleading insofar as the defining polynomial is irreducible and the surface, as a result, consists just of one algebraic component (not of two components as the figure suggests).
It can be shown that Calyx is an appropriate projection of Calypso. In a three-dimensional space a cylinder surface is contracted to the singular straight line of Calyx. Algebraically, the mapping is defined by the requirement (x, y, z) → (xz, y, z). It is very simple. The respective substitution in x2+y2z3 = z4 and subsequent reducing of z2 yields the Calypso equation x2+y2z = z2.
Papatya
Papatya’nın denklemi şöyle: (x2−y3)2 = (z2−y2)3. Türev alarak tekilliklerinin nerede olduğuna bakarsak tekil noktalar kümesinin düzlemsel iki eğriden oluştuğunu görüyoruz. Bu eğriler bir noktada kesişiyorlar, o noktada birbirlerine teğet değiller ve o nokta ikisinin de bir tekillik noktası. Tekil noktaları daha iyi anlayabilmek için, geometriciler o noktalarda yüzeyi patlatır ve çözünüm yüzeyini inşa ederler. Birkaç patlatma adımından sonra çözünüm yüzeyi pürüzsüz hale gelir (manifold), ortada tekillik kalmaz. Bu pürüzsüz yüzeyden orijinal yüzeye izdüşüm fonksiyonu sayesinde, orijinal yüzeyi manifoldun bir gölgesi olarak yorumlayabiliriz.
Diabolo
The Diabolo equation x2 = (y2+z2)2 factorizes into the product (x−y2−z2)(x+y2+z2) = 0. Hence, the respective surface is the unification of the two single-shell rotating hyperboloids x = ±(y2+z2). They touch each other tangentially at the origin. The contact can algebraically be gathered from the concurrent linear term x in the two factors. The tangent plane is the vertical plane x = 0.
The stripes in the images are shades due to lighting. If you modify the Diabolo equation by adding a constant term such as in x2 = (y2+z2)2+1/1000, then the two halves are separated. The substitution of x by x+y, however, yields the variation (x+y)2 = (y2+z2)2 of the equation. The two shells are moved at an angle to each other.
Ding Dong
This surface described by the equation x²+y²+z³ = z² was one of the very first visualizations we tried. Equation and shape are simple: A vertical alpha-loop rotates around the z-axis. But there was the problem with the colouring. Green is generally rather tricky in three-dimensional visualization of surfaces and, in addition, tends to be matt or yellowish. The lights and reflexions must be well tested. Note the light blue hard shadow intensifying the spatial effect.

Formül
- x^2+y^2+z^2+1500\cdot(x^2+y^2)\cdot(x^2+z^2)\cdot(y^2+z^2)-1=0
Pıtrak
x2 + y2 + z2 + c (x2+y2)(x2+z2)(y2+z2) = 1 formülüyle elde edilmiş Pıtrak yüzeyi, sıradışı simetrisiyle dikkat çekmektedir. Burada gördüğünüz halini elde etmek için çok büyük bir c katsayısı seçmek gerekiyor. Pıtrak’ın altı dikeni, Öklit uzayının üç koordinat ekseni üzerinde yer almaktadır. Üç ekseni birbirine götüren herhangi bir uzay döndürmesi, Pıtrak’ı olduğu gibi yerinde bırakır. Bu yüzden Pıtrak’ın simetri grubu küpünkiyle ve ona düal cisim olan sekizyüzlününkiyle aynıdır. Bunlar, yalnızca beş adet olan Platon cisimlerinin ikisidirler.
İşin şaşırtıcı tarafı, Pıtrak gibi mükemmel simetrisi olan ve herhangi sayıda diken içeren cebirsel bir yıldız yapmak olası değildir. Bu sonuç, cebirdeki Grup Kuramından gelir. Yalnızca 4, 8, 12 ya da 20 diken yaratabilirsiniz; bu sayılar da Platon yüzeylerinin yüz sayısıdır. Meraklı gözlere, bu yıldızların formüllerini bulmayı bir alıştırma olarak bırakıyoruz.
Dullo
If the audience in an oval stadium scream about a score (typically of the favoured team), the sound spreads like a quickly inflated floating tyre. After some split seconds the tyre meets itself at its centre – the opening has closed – and that is what exactly happens at the kick-off spot. At that point sound waves from all directions meet simultaneously and are boosted accordingly. This is why referees are advised to always stay level with the ball. Thus, when a goal is scored they do not stand in the middle circle and get a buzzing in their ears.
Eistüte (Cone)
The horizontal section through Cone is a so-called rosette curve: A small wheel rolls round the interior of an annular body while a pencil fixed to the wheel is drawing a curve (like a Spirograph).
Different curves are formed depending on the ratio of the two radii. The curve closes if the ratio is a rational number.
In our case it is the four- leaf clover. Our cone has the advantage that four scoops of ice-cream will fit in!
Helix
The Lemniscate is the plane curve with the equation y4+z2 = y2. It results from the circle y2+z2 =1 by substituting z by z/y. Geometrically, the substitution corresponds to a distortion of the circle to a figure of eight loop. If y4+z2 = y2 is conceived as equation with three variables x, y and z (where x is hidden) then the solution set is a surface in the three-dimensional space, i. e. the cylinder above the lemniscate.
The Helix equation y4+x2z2 = y2 is yielded by substituting z by xz. From the geometrical view, this construction is a kind of folding. The symmetry with respect to x and z is clearly visible. For the final formula we added the factors 2 and 6 to slightly stretch Helix. The singular locus is a crossing of straight lines. The sections of Helix with the planes x = c or z = c are lemniscates for c ≠ 0, whereas the sections y = c are hyperbola pairs.
Herz (Heart)
Despite the simple equation y2+z3 = z4+x2z2 the surface Heart possesses a subtle local and global structure. The singular set is a straight line on which the surface intersects itself. The origin 0 is the interesting point as we intersect Heart with planes x = c orthogonal to the singular straight line. The result is a loop which contracts like a knot if c tends to 0. A funnel is formed.
Viewed from the distance we see a circle shaped opening in the surface. The section with the vertical xy-plane is in fact a circle. The simplicity of the surface allows us to close our eyes, yet still recall the figure in detail. However, it is much more difficult to describe verbally the geometric pattern because there are no common words to do so.
Himmel & Hölle (Heaven and Hell)
A piece of paper is folded and is held from beneath such that you can put your four fingers in the four corners so formed. By spreading your fingers the figure opens in two different ways so that two of the four inner sides can be seen at a time.
This figure reminds us of the popular children’s fortune teller game where you have to predict which colour will show up – blue for heaven and red for hell (hence the name!)
By adding up the squares at y and z you get the highest exponent 4. This is called an equation of the 4th degree. The higher the degree the more complicated it is to calculate the surface.
Kolibri (Hummingbird)
You may notice that Hummingbird is a close-up, upside down view of Heart near the origin. The equation is x3+x2z2 = y2, compared with the Heart formula y2+z3 = z4+x2z2. It is possible to change the coordinates so that one transforms into the other.
The Hummingbird is one of the smallest birds and is equipped with impressive abilities. Its wings are able to beat up to 200 times in a second so that it can hover in the air. This activity needs a lot of energy, and is why the hummingbird must eat twice its body weight in food per day. Without constant food supply it would starve within a few hours. It lowers its body temperature substantially at night so as to save energy.
Kreisel (Spinning Top)
To illustrate the shape of a spinning top as a solution set of a simple algebraic equation needs some inventive mathematics! It is, indeed, not clear mathematically, at first sight, what this equation must look like because different equations can provide similar looking forms.
The image shows the equation 60(x2+y2)z4 = (60−x2−y2−z2)3. The rotation symmetry round the vertical z axis is identified by x and y occurring in the quadratic polynomial x2+y2. The third power on the right hand side is necessary to produce the two points. And as z occurs only in even powers, the surface is symmetrical with respect to the reflection in the horizontal xy plane. The parameter 60 in the equation is used for aesthetic reasons.
Miau
This surface was developed by chance on a dull train journey (working with algebraic visualisation makes time pass more quickly on boring train rides!).
Deriving the algebraic equation for this surface would be very difficult. The challenge of Miau is the double opening with embedded singularity.
For mathematicians this is a treasure trove exploring the relationship between equation and form.
Nepali
Let us look at the defining equation (xy−z3−1)2 = (1−x2−y2)3 of Nepali. The symmetry between x and y is enforced by the quadratic polynomial x2+y2, which is rotation symmetrical in contrast to the monomial xy. Sections with horizontal planes z = c yield closed curves being almost circles. The simultaneous occurrence of squares and third powers produces the tapering at the top.
The lateral boundary curve of Nepali is not an exact circle but is arching up and down like the brim of a hat. Its projection to the horizontal xy plane, however, is a circle as can be seen from the top view. The surface shown is bounded; hence there was no need to limit the view by sphere intersection. This fact can be directly derived from the formula by accurate analysis.
Seepferdchen (Seahorse)
If you want to find the equation of this surface it would take strong efforts. The soft tangential contact is not easy to achieve. It vanishes as you only slightly change the formula.
The elegance of the sea horse is an illusion: If you look at it from behind or from the side, it appears quite clumsy. Sea horses live worldwide in tropical and temperate climate zones. Its Latin name is Hippocampus, you can find the equation next to it.
Solitude
The Solitude equation x2yz+xy2+y3+y3z = x2z2 does not reveal its hidden geometrical diversity. Similarly, the image shows only part of the phenomena. What is informative, however, is the camera drive round the surface as it can be experienced in the film “ZEROSET – I spy with my little eye”.
There are obviously two openings, a larger well visible one and a smaller one, which you would not suspect from the first perspective. The view from above shows the vertical singular straight line alongside which horizontal sections force a sharp curve. The example of Solitude shows the complexity of the problem to deduce the visible real geometry from the equation. Similarly, one can question the underlying complex or number-theoretical geometry.
Tanz (Dance)
By setting z = 0 the Dance equation 2x4 = x2 +y2z2 yields the equation 2x4 = x2. This is the section of Dance with the horizontal xy plane. If you rewrite the equation you will get x2(√2x+1) (√2x−1) = 0 of three parallel straight lines. We, here, observe a typically real phenomenon: The straight line x = z = 0 belongs to the solution set of the Dance equation 2x4 = x2+y2z2, but is an isolated one-dimensional component, because if x is near 0 there are only the solutions x = y = 0 or x = z = 0, that means the cross consisting of the y and z axis.
As straight lines are infinitely thin they are missed by the visualization program or are not indicated. Therefore, the existence of one-dimensional components in the solution set must be cleared up by computation beforehand and then they must be added to the image as thin cylinders, if necessary.
Taube (Dove)
Dove possesses the amazing formula
256z3 − 128x2z2+16x4z+144xy2z−4x3y2−27y4 = 0.
The coefficients are not incidental. On the contrary: The equation results from another more general formula, the so-called discriminant. It describes the shade of a surface or variety which emerges along with the projection on a surface or a linear space of higher dimension. The contour line is clearly defined by the surface and the projection and, from the algebraic point of view, also the form of the equation.
Tülle (Nozzle)
The Nozzle surface is constituted by three smooth components, which intersect each other pairwise in a (likewise) smooth, plane curve. That way, three section curves are obtained, i. e. one straight line and two parabolas. Note that these curves touch each other tangentially at the origin. We here have the simplest example of a surface with three pairwise transversal components so that the section curves of every two of them do not intersect transversally. The surface, thus, is no Mikado Variety.
The transversal intersection of two smooth components of a surface – a fundamental concept of geometry - can, by way of the so-called ideal theory, be put into formulas in an algebraically precise manner. It can perfectly be used for calculation and proofs. In the case of singular components a correct definition of transversality is still to await.
Zeck (Tick)
The simple Tick equation x2+y2 = z3(1−z) fully dictates the geometry just as with the other surfaces; that means, both the singular points and the outer shape, the curvature and the extension are clearly defined by the four monomials x2, y2, −z3 und z4. As a result, the formula is a very efficient way to codify forms which appear complicated. However, the geometric information cannot always be read from the formula. The local shape of the surface near a given point can be explicitly defined, in most cases; the techniques of local analytic geometry have a good effect. Defining the global structure requires much more efforts and cannot always be satisfactorily accomplished.