Ulrich Pinkall, Nicholas Schmitt, Charles Gunn et Tim Hoffmann
La géométrie différentielle est l’étude des formes courbées, telles que les lignes courbes, les surfaces dans l’espace, ou même des formes à plusieurs dimensions. En géométrie différentielle, les formes des bulles et des films de savon sont déterminées par leur «courbure moyenne» qui est alors la même en tout point de la surface. Plusieurs images de cette galerie représentent des surfaces à courbure moyenne constante, une image montre une surface qui n’est pas d’aire minimale mais de «courbure totale» minimale. Une autre image représente un espace tridimensionnel à courbure constante.
Surfaces minimales discrètes
Les surfaces minimales sont un sujet classique d’étude en géométrie différentielle. Ce sont des surfaces dont la courbure moyenne s’annule en tout point. Les surfaces les plus connues de cette classe sont le Caténoïde et l’Hélicoïde. Une des nombreuses propriétés remarquables des surfaces minimales est l’existence d’une famille associée. Cela signifie que les surfaces sont déformables tout en restant minimales (elles sont même isométriques entre elles et les plans tangents associés sont parallèles). L’Hélicoïde et le Caténoïde sont ainsi associés dans la même famille. Il en résulte qu’ils peuvent être déformés l’un en l’autre et les surfaces de transition restent minimales.
L’image illustre une discrétisation de la surface minimale à mi-chemin entre le Caténoïde et l’Hélicoïde. Elle est constituée de sphères et de cercles tangents entre eux. Il existe aussi une famille associée pour ces surfaces minimales discrètes. Les rayons des sphères correspondantes et les positions des disques circulaires sont préservés.
La trame a été développée avec jReality, l’image elle-même a été calculée par POV-Ray.
Espace hyperbolique
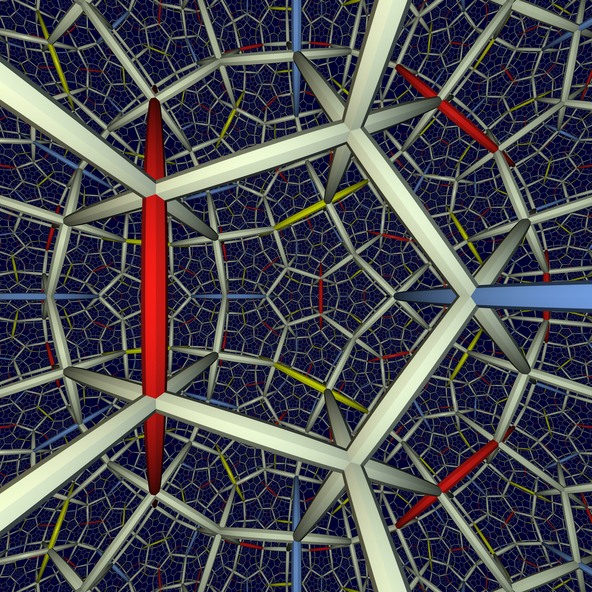
L’image offre une plongée dans l’espace hyperbolique de dimension 3 grâce à son remplissage par d’innombrables dodécaèdres réguliers. L’espace hyperbolique est un espace courbé de courbure négative. Cela signifie que les lignes parallèles divergent au lieu de rester à égale distance comme dans notre espace plat.
Les faces des dodécaèdres se rencontrent deux à deux en angle droit dans l’espace hyperbolique, ce qui n’est pas aisément visible à cause de notre habitude de la géométrie plate. De même que les cubes remplissant l’espace plat, on voit clairement ici huit solides se rencontrer en chaque sommet.
Le remplissage de l’espace hyperbolique par des dodécaèdres montré ci-dessus apparaît en topologie lorsque l’on essaye d’avoir une réalisation géométrique de l’espace ambiant des Anneaux Borroméens. Les faisceaux rouges, jaunes et bleus de l’image correspondent aux trois anneaux entrelacés. La figure montre la scène telle qu’un habitant de l’espace hyperbolique la percevrait. Des tentatives ont déjà été menées pour adapter les calculs pour les rayons lumineux en optique hyperbolique.
La trame a été développée avec jReality, l’image elle-même a été calculée par Renderman. Avec le soutien du DFG Research Centre Matheon.
Surface de Boy
La surface de Boy est formée par l’addition d’un ruban de Möbius à un disque dont on a recollé les bords respectifs en une surface fermée. La preuve qu’une telle construction est possible a été apportée par Werner Boy en 1901. La surface de Boy est lisse en dehors du lieu où elle s’intersecte elle-même.
La version illustrée ici est caractérisée par sa courbure moyenne aussi petite que possible, c’est-à-dire qu’elle n’a pas de «bosse superflue». Vous pouvez voir ici la plus «belle» réalisation possible d’une surface de Boy dans un sens mathématique précis. Il s’agit d’une paramétrisation de cette surface réalisée par Robert Bryant et Robert Kusner.
L’image est basée sur un panorama circulaire généré par Paul Debevec à partir de photos d’une église à San Francisco. La scène a été obtenue avec jReality, l’image elle-même calculée avec Sunflow. Avec le soutien du DFG-Research Centre Matheon.
Hélicoïde avec des anses
Une des surfaces minimales les plus connues est l’hélicoïde, que vous rencontrez au quotidien avec les escaliers en spirale et les rampes de parking. Il est en fait possible de connecter entre eux différents étages de l’hélicoïde sans détruire la propriété de surface minimale ni créer une surface s’intersectant elle-même. La partie connectée obtenue est appelée «anse» en vocabulaire mathématique. Suivant l’étage où vous vous trouvez, une telle anse ressemble à un trou dans le sol ou dans le plafond, ou encore à une colonne connectant le sol et le plafond d’un même étage. La surface illustrée ci-dessus est un hélicoïde à deux anses. Elle fut découverte et calculée par Markus Schmies.
L’image est basée sur un paysage généré par ordinateur en utilisant Terragen par Simon O’Callaghan. La scène a été développée avec jReality, l’image elle-même a été calculée par Sunflow. Avec le soutien du DFG Research Centre Matheon.
Nodoïde éclaté
Le nodoïde éclaté est une surface spéciale à courbure moyenne constante. Une telle surface peut être vue comme l’interface entre deux liquides ou deux gaz de pressions différentes à l’instar d’une bulle de savon renfermant un certain volume d’air. Contrairement aux bulles de savons réelles, on autorise les bulles de savon mathématiques à se recouper elles-mêmes. Imaginez que les cinq branches que l’on voit partir de la surface continuent indéfiniment. Un équilibre des forces est réalisé : les quatre tubes ondulants poussent l’extrémité supérieure vers le bas et maintiennent la colonne centrale poussant vers le haut en équilibre.
La surface a été calculée par Nicholas Schmitt (GeometrieWerkstatt Tübingen), qui a également conçu et calculé l’image en utilisant le logiciel XLab.
Tétranoïde
Le Tétranoïde appartient à la famille des surfaces qui ont les mêmes propriétés de courbure que les bulles de savon physiques. On dit en mathématiques que le Tétranoïde est à «courbure moyenne constante». Les quatre «jambes» du Tétranoïde sont en fait infinies.
L’existence du Tétranoïde (de même que l’existence de surfaces similaires à symétries basées sur les solides platoniciens) a été démontrée par Nicholas Schmitt, qui a également calculé la surface.
L’image est basée sur un panorama circulaire que Paul Bourke a généré à partir de photos. La scène a été compilée avec jReality, et l’image elle-même calculée avec Sunflow. Avec le soutien du DFG-Research Centre Matheon.
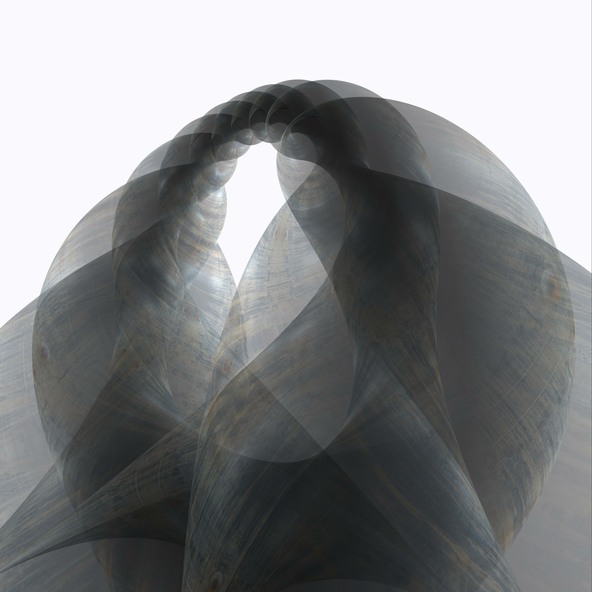
Tore tressé
Le Tore tressé est une surface anulaire à courbure moyenne constante dans la sphère de dimension trois, elle-même courbée. La mettre en évidence demande tout d’abord de la projeter dans notre espace plat. Heureusement, ceci est réalisable de sorte que les caractéristiques essentielles de la forme soient conservées. Inclus dans son espace de dimension trois, il possède une symétrie de vissage qui peut encore être maintenue lors de la projection.
Le Tore tressé n’est qu’un exemple simple parmi une infinité de surfaces annulaires toujours plus complexes ayant des propriétés de courbure semblables.
La surface a été développée par Nicholas Schmitt (GeometrieWerkstatt Tübingen), dont il a établi l’image en utilisant le logiciel XLab.
Surface de Björling
Les surfaces minimales sont des surfaces ayant les mêmes propriétés de courbure que les films de savon. En géométrie différentielle, la construction de surfaces minimales avec des caractéristiques données est un sujet classique. En 1844, E. G. Björling montra que pour toute courbe de l’espace suffisamment régulière, il existe une surface minimale formant une bande mince contenant la courbe. On peut de plus imposer a priori la manière qu’a la bande de se torsader autour de la courbe.
La surface illustrée ici est générée par une courbe en hélice autour de laquelle la bande est vrillée à vitesse constante.
Les formules décrivant cette surface de Björling particulière nous viennent de Matthias Weber. L’image est basée sur un paysage généré par ordinateur par Simon O’Callaghan à l’aide de Terragen. La scène a été développée avec jReality; l’image elle-même a été réalisée à l’aide de Sunflow. Avec le soutien du DFG-Research Centre Matheon.