Ulrich Pinkall, Nicholas Schmitt, Charles Gunn und Tim Hoffmann
In der Differentialgeometrie werden gekrümmte Formen untersucht, wie zum Beispiel krumme Linien oder Flächen im Raum oder sogar Formen mit mehr als drei Dimensionen. Man befasst sich hier mit Fragen wie: Was ist der Unterschied zwischen der Art, wie ein Ei gekrümmt ist, von der eines Kühlturms? Wie kann man Krümmung messen?
Besonders interessant sind Flächen, die in dem Sinne „optimal” sind, dass ein genau festgelegtes „Qualitätsmaß” nicht verbessert werden kann, wenn man kleine Änderungen an der Fläche vornimmt.
Zum Beispiel hat eine Seifenhaut, die man durch Eintauchen eines gebogenen Drahtes in Seifenlösung erhält, die kleinste Oberfläche unter allen möglichen Flächen, die man in den Draht einspannen kann. Seifenblasen minimieren den Flächeninhalt im Vergleich zu allen in sich geschlossenen Flächen, die ein bestimmtes Luftvolumen einschließen. Vom Standpunkt der Differentialgeometrie sind die Formen von Seifenhäuten und Seifenblasen dadurch ausgezeichnet, dass die so genannte „mittlere Krümmung” an jedem Flächenpunkt dieselbe ist.
Mehrere Bilder in dieser Galerie zeigen Flächen mit konstanter mittlerer Krümmung. Ein Bild zeigt eine Fläche, die keine minimale Oberfläche hat, sondern minimale „Gesamtkrümmung”. Ein weiteres Bild zeigt einen dreidimensionalen gekrümmten Raum mit konstanter Krümmung.
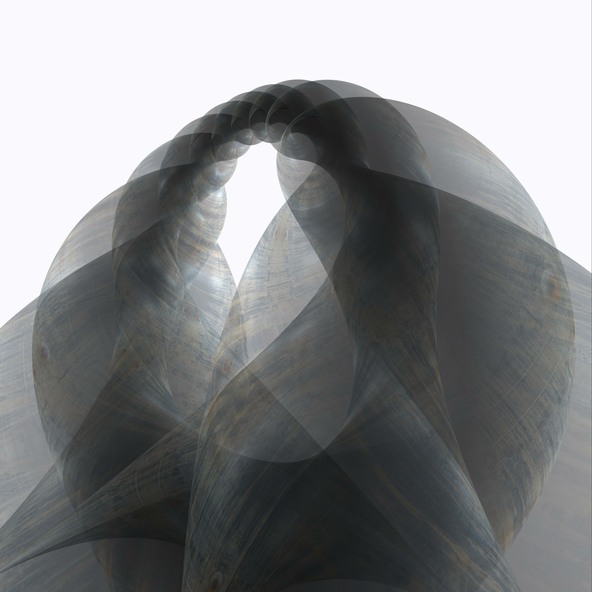
Diskrete Minimalfläche
Minimalflächen sind ein klassisches Untersuchungsobjekt der Differentialgeometrie. Es sind Flächen, deren mittlere Krümmung überall verschwindet. Zu den bekanntesten Vertretern dieser Flächenklasse gehören das Katenoid und das Helikoid. Eine der vielen interessanten Eigenschaften von Minimalflächen ist die Existenz einer assoziierten Familie. Dies ist eine Deformation, bei der die Flächen minimal bleiben (sie sind sogar isometrisch zueinander und entsprechende Tangentialebenen sind parallel). Helikoid und Katenoid gehören zu derselben assoziierten Familie. Man kann sie also ineinander deformieren und alle Flächen dazwischen sind ebenfalls minimal.
Das Bild zeigt eine Diskretisierung der Minimalfläche auf halbem Wege zwischen Katenoid und Helikoid. Sie ist aus sich berührenden Sphären und Kreisen durch die Berührpunkte zusammengesetzt. Auch für solche diskreten Minimalflächen gibt es eine assoziierte Familie, und sowohl die Radien entsprechender Sphären als auch die Stellungen entsprechender Kreisscheiben sind gleich.
Die Szene wurde in jReality zusammengestellt, das Bild selbst wurde mit POV-Ray berechnet.
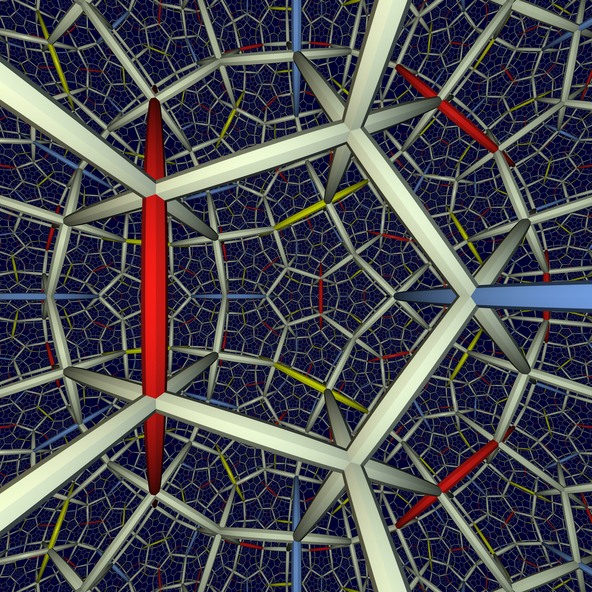
Hyperbolischer Raum
In dem Bild kann man einen Blick in den dreidimensionalen hyperbolischen Raum werfen, wie er durch unendlich viele reguläre Dodekaeder ausgefüllt wird. Der hyperbolische Raum ist ein gekrümmter Raum, und zwar mit negativer Krümmung. Dies bedeutet, dass er mit zunehmender Entfernung stärker auseinanderläuft, als unser flacher Raum. Die Flächen der Dodekaeder stoßen im hyperbolischen Raum mit rechten Winkeln aufeinander, was aber auf Grund unserer an die flache Geometrie angepassten Sehgewohnheiten nicht leicht zu sehen ist. Wie bei der Ausfüllung unseres flachen Raums durch Würfel treffen aber offenbar auch hier in jedem Eckpunkt acht Körper aufeinander. Die hier gezeigte Ausfüllung des hyperbolischen Raums durch Dodekaeder tritt in der Topologie auf, wenn man versucht, den umgebenden Raum der so genannten „Borromäischen Ringe“ geometrisch zu realisieren. Die roten, gelben und blauen Balken im Bild entsprechen den drei Ringen, die diese Verschlingung ausmachen. Das Bild zeigt die Szenerie so, wie sie auch ein Bewohner des hyperbolischen Raums wahrnehmen würde. Es ist sogar versucht worden, die Beleuchtungsberechnungen an die hyperbolische Optik anzupassen.
Die Szene wurde in jReality zusammengestellt, das Bild selbst wurde mit Renderman berechnet. Gefördert vom DFG-Forschungszentrum Matheon.
Boysche Fläche
Die Boysche Fläche ist eine nicht-orientierbare Fläche. Sie stellt eine mögliche Parametrisierung dar, die durch das Ankleben eines Möbiusbandes an den Rand einer Scheibe entsteht. Sie wurde 1901 von Werner Boy entdeckt und ist ein Modell der projektiven Ebene ohne Singularitäten (aber mit Selbstdurchdringungen). Vor dem Eingang des Mathematischen Forschungsinstituts Oberwolfach steht ein großes Modell der Boyschen Fläche. Es wurde von Mercedes-Benz 1991 konstruiert und gestiftet.
Die hier gezeigte Variante ist dadurch ausgezeichnet, dass ihre Krümmung im Mittelwert so klein wie möglich ist. Sie hat in diesem Sinne „keine überflüssigen Beulen“. Man sieht hier also in einem mathematisch präzisen Sinne die „schönste“ mögliche Realisierung der Boyschen Fläche. In dieser Form stammt die Boysche Fläche von Robert Bryant und Robert Kusner.
Das Bild benutzt ein Kugelpanorama, das Paul Debevec aus Fotos in einer Kirche in San Francisco erstellt hat. Die Szene wurde in jReality zusammengestellt, das Bild selbst wurde mit Sunflow berechnet. Gefördert vom DFG-Forschungszentrum Matheon.
Helikoid mit Henkeln
Minimalflächeneigenschaft zu zerstören oder zu bewirken, dass die Fläche beginnt, sich selbst zu durchdringen. Mathematisch bezeichnet man ein solches Verbindungsstück als „Henkel“. Je nachdem, in welcher Etage man steht, sieht ein solcher Henkel aus wie ein Loch in Boden oder Decke, oder auch wie eine Säule, die Boden und Decke einer Etage verbindet.
Die hier gezeigte Fläche ist ein Helikoid mit zwei Henkeln und ist von Markus Schmies gefunden und berechnet worden. Das Bild benutzt eine Computer-generierte Landschaft, die Simon O‘Callaghan mit Terragen erstellt hat. Die Szene wurde in jReality zusammengestellt, das Bild selbst wurde mit Sunflow berechnet. Gefördert vom DFG-Forschungszentrum Matheon.
Aufbrechendes Nodoid
Das aufbrechende Nodoid ist eine besondere Fläche mit konstanter mittlerer Krümmung. Man kann sich eine solche Fläche vorstellen als Grenzfläche zwischen zwei Flüssigkeiten oder Gasen mit verschiedenem Druck, wie zum Beispiel eine Seifenblase, die ein bestimmtes Luftvolumen einschließt. Im Unterschied zu physikalischen Seifenblasen dürfen mathematische Seifenblasen sich aber selbst durchdringen.
Man muss sich vorstellen, dass alle fünf Ausläufer, die man von der Fläche ausgehen sieht, bis ins Unendliche weitergehen. Dabei besteht ein Kräftegleichgewicht: Die vier welligen Rohre ziehen das obere Ende nach unten und halten so der mittleren Säule das Gleichgewicht, die nach oben drückt.
Die Fläche wurde von Nicholas Schmitt (GeometrieWerkstatt Tübingen) gefunden, und er hat auch das Bild mit der Software XLab entworfen und berechnet.
Tetranoid
Das Tetranoid gehört zu einer Klasse von Flächen, welche dieselben Krümmungseigenschaften haben wie physikalische Seifenblasen. Mathematisch sagt man: das Tetranoid hat „konstante mittlere Krümmung”. Die vier „Beine“ des Tetranoids gehen eigentlich bis ins Unendliche weiter.
Die Existenz des Tetranoids (ebenso wie die Existenz von ähnlichen Flächen mit beliebigen auf den Platonischen Körpern beruhender Symmetrie) wurde von Nicholas Schmitt bewiesen, er hat auch die Fläche berechnet.
Das Bild benutzt ein Kugelpanorama, das Paul Bourke aus Fotos erstellt hat. Die Szene wurde in jReality zusammengestellt, das Bild selbst wurde mit Sunflow berechnet. Gefördert vom DFGForschungszentrum Matheon.
Twizzle-Torus
Der Twizzle Torus ist eine Ringfläche mit konstanter mittlerer Krümmung in der dreidimensionalen Sphäre, einem in sich gekrümmten Raum. Um ihn sichtbar zu machen, muss er zuerst in unseren flachen Raum projiziert werden. Dies ist zum Glück so möglich, dass grundlegende Formeigenschaften erhalten bleiben. In der dreidimensionalen Sphäre, wo er zu Hause ist, hat er eine Schraubsymmetrie, die auch in der Projektion noch ahnbar ist.
Der Twizzle Torus ist nur ein relativ einfaches Exemplar in einer unendlichen Hierarchie von zunehmend komplexen Ringflächen mit ähnlichen Krümmungseigenschaften.
Die Fläche wurde von Nicholas Schmitt (GeometrieWerkstatt Tübingen) gefunden, und er hat auch das Bild mit der Software XLab entworfen und berechnet.
Björling-Fläche
Minimalflächen sind Flächen, die dieselben Krümmungseigenschaften haben wie physikalische Seifenhäute. Die Konstruktion von Minimalflächen mit vorgegebenen Eigenschaften ist ein klassisches Thema der Differentialgeometrie. E. G. Björling hat 1844 gezeigt, dass man zu jeder genügend gutartigen Raumkurve einen schmalen Minimalflächenstreifen finden kann, der die Kurve enthält. Zusätzlich kann man sogar noch vorschreiben, wie sich der Streifen um die Kurve winden soll.
Die hier gezeigte Fläche entsteht auf die genannte Weise, wenn man als Ausgangskurve eine Helix nimmt, längs der man mit fester Geschwindigkeit den Streifen verdrillt.
Die Formeln für diese spezielle Björling Fläche stammen von Matthias Weber. Das Bild benutzt eine computergenerierte Landschaft, die Simon O’Callaghan mit Terragen erstellt hat. Die Szene wurde in jReality zusammengestellt, das Bild selbst wurde mit Sunflow berechnet. Gefördert vom DFG-Forschungszentrum Matheon.