Ulrich Pinkall, Nicholas Schmitt, Charles Gunn y Tim Hoffmann
La geometría diferencial es el estudio de formas curvas, como líneas o superficies curvas, o incluso formas de más dimensiones. Desde el punto de vista de la geometría diferencial las pompas y películas de jabón adquieren su forma porque la denominada «curvatura principal» es igual en cada punto de la superficie. En esta galería se presentan varias imágenes de superficies de curvatura principal constante, una de ellas muestra una superficie que no tiene área minimal pero sí «curvatura total» minimal. En otra se ve un espacio tridimensional de curvatura constante.
Discrete Minimal Surface
Películas de jabón
Si se introduce un alambre alabeado cerrado en un líquido jabonoso, al sacarlo se obtiene una película. Debido a la tensión superficial del líquido, esta película es una superficie en equilibrio, lo que además implica que es una superficie de área mínima, entre las que tienen el mismo borde (el alambre). Geométricamente, esta propiedad es equivalente a que la curvatura media H sea nula. A las superficies con esta propiedad se las llama superficies minimales. Primeros ejemplos: el helicoide (escalera de caracol) y el catenoide (superficie de revolución de la catenaria). Además, éstas pueden ser deformadas una en la otra a través de una familia de superficies que siguen siendo minimales.
En esta imagen (del matemático Tim Hoffman) se muestra la discretización de una superficie minimal intermedia de dicha familia. La representación o el dibujo de superficies “suaves” utilizando círculos o discos planos (discretización) es una herramienta potente en visualización, arquitectura y diseño.
Hyperbolic Space
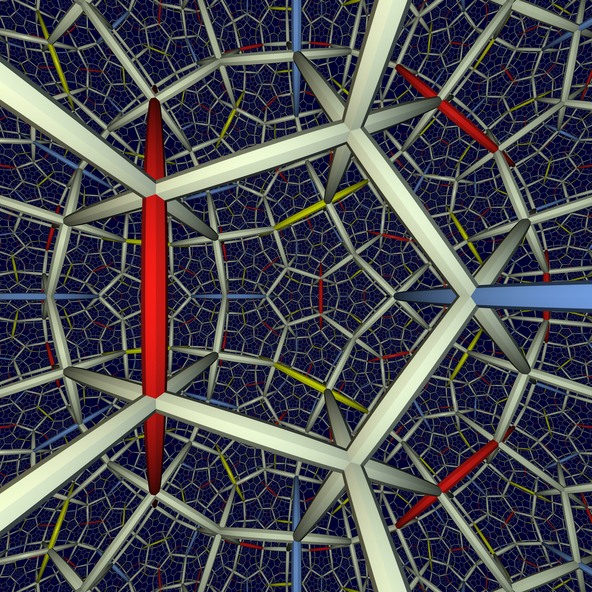
Posibilidades hiperbólicas / Donde con dodecaedros se puede recubrir el espacio
El espacio euclidiano ordinario no se puede recubrir (la palabra usada en matemáticos es teselar) con dodecaedros regulares. Es imposible por las mismas razones que un plano euclidiano se puede teselar con triángulos, cuadrados y hexágonos regulares, pero no con pentágonos regulares (el ángulo interior en un vértice del pentágono regular es 108º, que no divide a 360º). Pero existen planos y espacios llamados hiperbólicos que se pueden teselar por pentágonos y dodecaedros regulares, respectivamente. Esto es posible debido a que estos espacios tienen ‘curvatura’, lo cual conlleva, por ejemplo, que existen pentágonos regulares cuyos ángulos interiores son rectos, y estos pentágonos ‘se pegan’ tan bien en el plano hiperbólico como los cuadrados en el plano euclidiano. La figura representa la teselación con dodecaedros regulares del espacio hiperbólico, que ‘se pegan’ tan bien como los cubos en el espacio euclidiano.
Boy Surface
Superficie de Boy / Sombras desde la 4D
l ejemplo por antonomasia de superficie no orientable cerrada (sin borde) es el llamado plano proyectivo. Este surge, con la geometría proyectiva, en el Renacimiento, en el estudio de la perspectiva en pintura, y puede pensarse como el espacio de todas las direcciones en las que los rayos paralelos de luz pueden crear sombras. El plano proyectivo es una superficie muy importante en matemáticas, pero difícil de imaginar, puesto que solamente se puede visualizar en la cuarta dimensión (4D).
La superficie de Boy es un modelo en nuestro espacio tridimensional del plano proyectivo, que se genera pegando, a través de sus bordes, un disco y una banda de Moebius. La Superficie de Boy se corta a si misma, pero es suave en cada uno de sus puntos. La versión que se muestra aquí se caracteriza por tener una curvatura media H lo más pequeña posible, es decir, “no tiene protuberancias innecesarias”, lo que realza su belleza.
Helicoid with Handles
Helicoide … con asas
El helicoide es la superficie formada por las infinitas rectas que unen los puntos de una hélice circular con los de su eje central y son perpendiculares a este eje.
Es muy habitual en nuestra vida: escaleras de caracol, tuercas, tornillos, móviles de viento o los “tornillos de Arquímedes”. Este mecanismo, formado por un helicoide que gira dentro de un cilindro, ha sido utilizado desde la antigüedad para diseñar máquinas destinadas al desplazamiento de líquidos (subir agua a un nivel más alto) y sólidos (arena, harina, cereales o cremas). Esta forma se ha usado profusamente en arquitectura.
Puede obtenerse como una película jabonosa con un alambre formado por una hélice cerrada al unirla a su eje. Esta imagen, diseño de Ulrich Pinkall, muestra un helicoide en el que se ha conseguido conectar los diferentes niveles del mismo sin romper la minimalidad de la superficie, ni provocar que la nueva superficie se corte a sí misma. La pieza de conexión se denomina, en matemáticas, “asa” y dependiendo de dónde se encuentra parecerá un agujero en el suelo o en el techo, o una columna que conecta los distintos niveles.
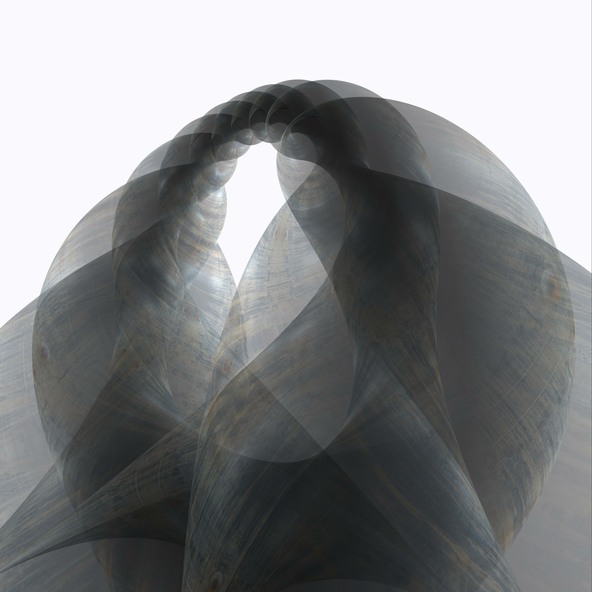
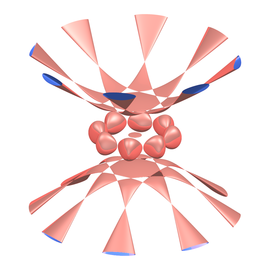
Bursting Nodoid
El nodoide en explosión es una superficie especial con una curvatura media constante. Dicha superficie puede imaginarse como una superficie límite entre dos líquidos o gases a diferente presión como una burbuja de jabón que encierra un cierto volumen de aire. En contraste con las burbujas de jabón físicas las burbujas de jabón matemáticas pueden intersectarse a sí mismas.
Tienes que imaginar que todas las cinco extensiones que ves emanando de la superficie continúan sin final. Y se logra un balance de fuerzas: Los cuatro tubos undulados llevan el extremo superior hacia abajo y así mantienen la columna media presionando hacia arriba en estado de balance.
La superficie fue desarrollada por Nicholas Schmitt (GeometrieWerkstatt Tübingen) y también diseñó y calculó la imagen usando el XLab software.
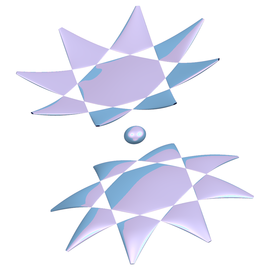
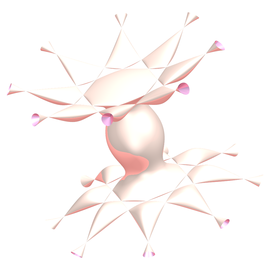
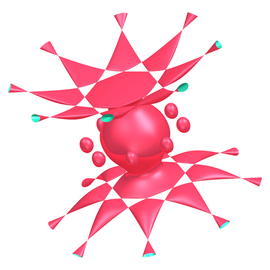
Tetranoid
Bombolles de sabó
El tetranoide pertany a la família de les superfícies amb curvatura mitjana H constant, que són el model geomètric de les bombolles de sabó. Igual que les superfícies minimals, són superfícies en posició d’equilibri, però ara la pressió a un costat i a l’altre no és necessàriament igual (per exemple, una gota d’oli en aigua). De la mateixa manera, aquestes superfícies són d’àrea mínima, però entre “les que tanquen un mateix volum”.
L’exemple per antonomàsia de superfície amb curvatura mitjana constant és l’esfera (la forma estable de la bombolla de sabó). Un altre exemple és la superfície d’una gota de líquid sobre una superfície plana, que en equilibri tindrà curvatura mitjana constant. L’estudi d’aquestes superfícies (minimals i de curvatura mitjana constant) és important en camps en què hi haja contacte entre dos medis (en microbiologia, mescla o separació de substàncies, prospeccions petrolíferes…).
El tetranoide és un nou exemple de superfície de curvatura mitjana constant, que ha estat construït per tenir simetria basada en el tetraedre (la piràmide de base triangular).
Twizzle Torus
Toro revolvente
El toro revolvente es una superficie anular con una curvatura media constante en la esfera tridimensional, un espacio curvado en sí mismo. Para hacerlo visible primero debe estar proyectado en nuestro espacio plano. Afortunadamente, esto está configurado de tal modo que las características de las formas básicas pueden mantenerse. En la esfera tridimensional donde pertenece tiene una simetría helicoidal que todavía puede ser conjeturada durante la proyección.
El toro revolvente es sólo un ejemplo comparativamente sencillo en una jerarquía interminable de superficies anulares cada vez más complejas con características de curvatura similares.
La superficie fue desarrollada por Nicholas Schmitt (GeometrieWerk- statt Tübingen) y él ha diseñado y calculado la imagen usando el software XLab.
Björling Surface
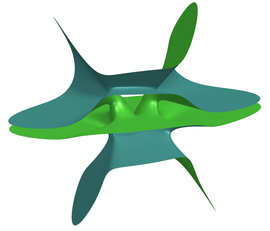
Superficie de Björling / Explorando nuevos territorios
Las superficies minimales son un modelo geométrico para las películas de jabón y se caracterizan por tener curvatura media H nula en todo punto de la superficie. Esta familia de superficies es un campo activo de investigación dentro de la Geometría Diferencial, con muchas aplicaciones industriales y tecnológicas, e incluso artísticas.
Un problema abierto es la construcción de nuevos ejemplos de superficies minimales, así como la obtención de nuevas técnicas para generarlos. En 1844 el matemático sueco E. G. Björling demostró que para cada curva alabeada espacial, suficientemente buena, podría construirse una banda de superficie minimal alrededor de la curva.
La superficie mostrada aquí (diseño de Ulrich Pinkall haciendo uso del programa jReality, a partir de las fórmulas matemáticas de Mathias Weber) es una superficie minimal de Björling generada a partir de una hélice.