Turtle Geometry
갤러리
Turtle Geometry
거북 기하(Turtle geometry, 역주: 거북이 앞으로 이동 및 회전하는 조작들만을 이용해 도형을 그리는 프로그램)가 여러 복잡한 대칭적 패턴들을 만들어 내는 데에 사용됩니다. 선들의 각도의 변화는 정해진 규칙들을 따릅니다. 선들 위에 특수함수들을 사용하여 형형색색의 배경을 칠할 수 있습니다.

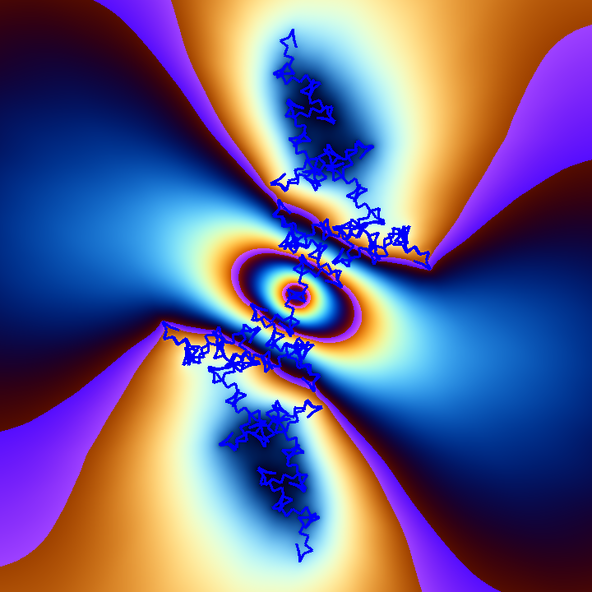
공식
- \varphi_{i+1} = \varphi_i + 170.5° \cdot i+180°
거북기하 작품 1
저작권 CC BY-NC-SA-3.0
공식
- \varphi_{i+1} = \varphi_i + 165.5° \cdot i+180°
거북기하 작품 2
저작권 CC BY-NC-SA-3.0

공식
- \varphi_{i+1} = \varphi_i + 71.5° \cdot i+180°
거북기하 작품 3
저작권 CC BY-NC-SA-3.0

공식
- \varphi_{i+1} = \varphi_i + 5.5° \cdot i+180°
거북기하 작품 4
저작권 CC BY-NC-SA-3.0

공식
- \varphi_{i+1} = \varphi_i + 60° \cdot i^2-180°
거북기하 작품 5
저작권 CC BY-NC-SA-3.0

공식
- \varphi_{i+1} = \varphi_i + 30° \cdot i^2-180°
거북기하 작품 6
저작권 CC BY-NC-SA-3.0

공식
- \varphi_{i+1} = \varphi_i + 150° \cdot i^2-180°
거북기하 작품 7
저작권 CC BY-NC-SA-3.0

공식
- \varphi_{i+1} = \varphi_i + 20° \cdot i^2-180°
거북기하 작품 8
저작권 CC BY-NC-SA-3.0

공식
- \varphi_{i+1} = \varphi_i + 40° \cdot i^2-180°
|
|
거북기하 작품 9
Turtle Geometry engages students in exploring mathematical properties visually via a simple programming language. This example shows a polygonal line consisting of a series of points connected by lines with unit length. The coordinates of each pointare calculated iteratively following simple rules.
The result is a beautiful figure with sixfold symmetry. By modification of the parameters interesting figures of different shape and symmetry are obtained.
저작권 CC BY-NC-SA-3.0

공식
- \varphi_{i+1} = \varphi_i + 100° \cdot i^2-180°
거북기하 작품 10
저작권 CC BY-NC-SA-3.0

공식
- \varphi_{i+1} = \varphi_i + 160° \cdot i^2-180°
거북기하 작품 11
저작권 CC BY-NC-SA-3.0

공식
- \varphi_{i+1} = \varphi_i + 15° \cdot i^2-180°
거북기하 작품 12
저작권 CC BY-NC-SA-3.0

공식
- \varphi_{i+1} = \varphi_i + 75° \cdot i^2-180°
거북기하 작품 13
저작권 CC BY-NC-SA-3.0

공식
- \varphi_{i+1} = \varphi_i + 105° \cdot i^2-180°
거북기하 작품 14
저작권 CC BY-NC-SA-3.0

공식
- \varphi_{i+1} = \varphi_i + 90°/7 \cdot i^2-180°
거북기하 작품 15
저작권 CC BY-NC-SA-3.0

공식
- \varphi_{i+1} = \varphi_i + 84° \cdot i^2-180°
거북기하 작품 16
저작권 CC BY-NC-SA-3.0

공식
- \varphi_{i+1} = \varphi_i + 132° \cdot i^2-180°
거북기하 작품 17
저작권 CC BY-NC-SA-3.0

공식
- \varphi_{i+1} = \varphi_i + 168° \cdot i^2-180°
거북기하 작품 18
저작권 CC BY-NC-SA-3.0

공식
- \varphi_{i+1} = \varphi_i + 78.75° \cdot i^2-180°
거북기하 작품 19
저작권 CC BY-NC-SA-3.0

공식
- \varphi_{i+1} = \varphi_i + 10° \cdot i^2-180°
거북기하 작품 20
저작권 CC BY-NC-SA-3.0

공식
- \varphi_{i+1} = \varphi_i + 50° \cdot i^2-180°
거북기하 작품 21
저작권 CC BY-NC-SA-3.0

거북기하 작품 22
저작권 CC BY-NC-SA-3.0

거북기하 작품 23
저작권 CC BY-NC-SA-3.0

거북기하 작품 24
저작권 CC BY-NC-SA-3.0

거북기하 작품 25
저작권 CC BY-NC-SA-3.0

거북기하 작품 26
저작권 CC BY-NC-SA-3.0

거북기하 작품 27
저작권 CC BY-NC-SA-3.0

거북기하 작품 28
저작권 CC BY-NC-SA-3.0

거북기하 작품 29
저작권 CC BY-NC-SA-3.0

거북기하 작품 30
저작권 CC BY-NC-SA-3.0

거북기하 작품 31
저작권 CC BY-NC-SA-3.0

거북기하 작품 32
저작권 CC BY-NC-SA-3.0

거북기하 작품 33
저작권 CC BY-NC-SA-3.0

거북기하 작품 34
저작권 CC BY-NC-SA-3.0

거북기하 작품 35
저작권 CC BY-NC-SA-3.0

거북기하 작품 36
저작권 CC BY-NC-SA-3.0

거북기하 작품 37
저작권 CC BY-NC-SA-3.0

거북기하 작품 38
저작권 CC BY-NC-SA-3.0

거북기하 작품 39
저작권 CC BY-NC-SA-3.0

거북기하 작품 40
저작권 CC BY-NC-SA-3.0

거북기하 작품 41
저작권 CC BY-NC-SA-3.0

거북기하 작품 42
저작권 CC BY-NC-SA-3.0

거북기하 작품 43
저작권 CC BY-NC-SA-3.0

거북기하 작품 44
저작권 CC BY-NC-SA-3.0





























































































