Circle Packing Explorations
서로 접하는 원들을 구성하는 데에는 여러 가지 방법이 있습니다. 하나는 아폴로니안 개스킷(Apollonian Gasket)이라 불리는 방법으로, 접하는 원 사이의 공간을 재귀적으로 채워 나가는 방식입니다. 하지만 이 방법은 초기의 원들 내부에 빈 공간을 크게 남깁니다. 이 빈 원들을 다시 같은 알고리즘을 이용해서, 매개변수를 변형하고 약간의 무작위성을 동반해 채워 나가는 아이디어를 추가하였습니다.
스타이너 사슬(Steiner Chain)이라 불리는 다른 방식은 두 원 사이에 서로 접하는 원들의 사슬을 채워 넣는 것입니다.
위 두 방식을 약간의 무작위성을 동반해 조합하면 무수히 많은 모양들을 얻을 수 있습니다.
다음 논문은 이 주제에 대해 더 잘 이해하는데 도움을 줄 것입니다:
http://www. lifl.fr/~decomite/papers/circlePacking.pdf
이 탐구의 프로그래밍 부분도 상당히 흥미롭습니다.

원 채우기: 탐구 1
이 예시는 원들의 배치 후에 약간의 뫼비우스 변환(Mobius transform)을 적용하였습니다. 뫼비우스 변환은 원을 원으로 보내고, 접하는 관계도 보존합니다. 이를 포함해서 이러한 디자인에 변화를 주기 위한 여러 가지 도구들을 활용합니다.
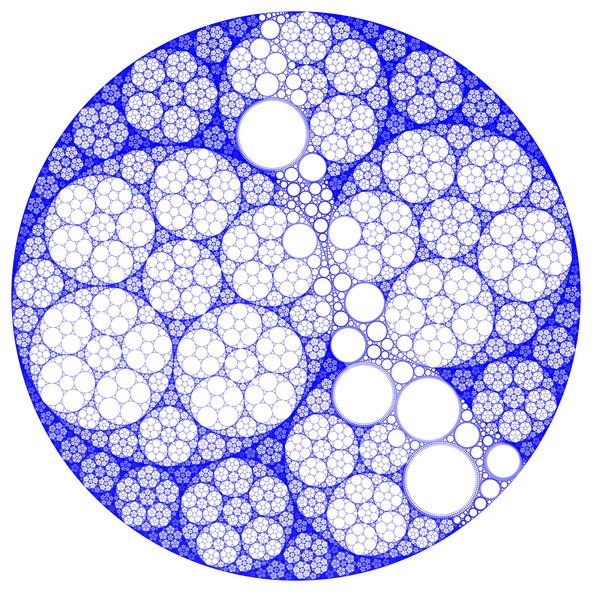
재귀적 아폴로니안 개스킷
최선의 결과가 나오진 않았지만, 다른 이미지들의 패턴 형성 과정들을 이해하는 데에 도움이 될 것입니다. 그림을 확대 관찰하며 알고리즘을 이해해 보세요.
짙은 보라색 위의 쉐이드
여기에선 뫼비우스 변환이 전체를 뒤집는 반전으로 작용했습니다. 원래 중심으로부터 아주 멀리 떨어져 있던 보라색 원들 중심으로 옮겨 놓은 것입니다. 그림 중간에 카마이외 배색(camaieu)을 형성하는 좋은 방법입니다.

악마의 언덕
2차원에서 신나게 원들을 갖고 노는 것에 더해, 3차원을 추가하는 것은 어떨까요? 이 그림에선 원들은 가우스 함수로 높이가 계산된 원기둥으로 대체됩니다.









