Jean-Francois Colonna - Deterministic Fractal Geometry
결정적 프랙탈 기하학의 그림들

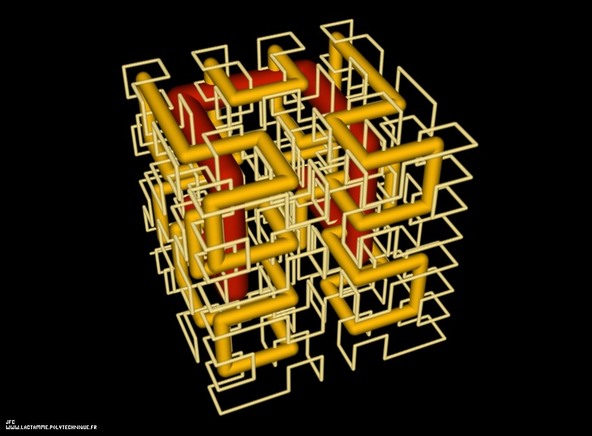
The Menger sponge -iteration 5-.
멩거 스펀지(Menger sponge)의 정의: 정육면체는 3x3x3=27개의 동일한 작은 정육면체들로 잘립니다. 그 후 중심의 하나와 면의 중심에 있는 6개의, 총 7개의 정육면체가 제거됩니다. 이 과정은 남은 20개의 작은 정육면체들에 반복됩니다. 멩거 스펀지의 프랙탈 차원은 다음처럼 주어집니다:
log(20)/log(3) = 2.726833027860842

An amazing cross-section inside the Menger sponge -iteration 5-.
멩거 스펀지(Menger sponge)의 정의: 정육면체는 3x3x3=27개의 동일한 작은 정육면체들로 잘립니다. 그 후 중심의 하나와 면의 중심에 있는 6개의, 총 7개의 정육면체가 제거됩니다. 이 과정은 남은 20개의 작은 정육면체들에 반복됩니다. 멩거 스펀지의 프랙탈 차원은 다음처럼 주어집니다:
log(20)/log(3) = 2.726833027860842
멩거 스펀지의 이 놀라운 단면은 다음 식으로 만들어 질 수 있습니다:
2X - 2Y + 2Z - 1 = 0
An amazing cross-section inside the Menger sponge -iteration 5- with a (4xO+1)/(1xO-1) conformal transformation in the Octonionic space -tridimensional cross-section-.
멩거 스펀지(Menger sponge)의 정의: 정육면체는 3x3x3=27개의 동일한 작은 정육면체들로 잘립니다. 그 후 중심의 하나와 면의 중심에 있는 6개의, 총 7개의 정육면체가 제거됩니다. 이 과정은 남은 20개의 작은 정육면체들에 반복됩니다. 멩거 스펀지의 프랙탈 차원은 다음처럼 주어집니다:
log(20)/log(3) = 2.726833027860842
멩거 스펀지의 이 놀라운 단면은 다음 식으로 만들어 질 수 있습니다:
2X - 2Y + 2Z - 1 = 0
An amazing cross-section inside the Menger sponge -iteration 5- with a 1/O conformal transformation in the Octonionic space -tridimensional cross-section-.
멩거 스펀지(Menger sponge)의 정의: 정육면체는 3x3x3=27개의 동일한 작은 정육면체들로 잘립니다. 그 후 중심의 하나와 면의 중심에 있는 6개의, 총 7개의 정육면체가 제거됩니다. 이 과정은 남은 20개의 작은 정육면체들에 반복됩니다. 멩거 스펀지의 프랙탈 차원은 다음처럼 주어집니다:
log(20)/log(3) = 2.726833027860842
멩거 스펀지의 이 놀라운 단면은 다음 식으로 만들어 질 수 있습니다:
2X - 2Y + 2Z - 1 = 0
The complement of the Menger sponge -iteration 5-.
멩거 스펀지(Menger sponge)의 정의: 정육면체는 3x3x3=27개의 동일한 작은 정육면체들로 잘립니다. 그 후 중심의 하나와 면의 중심에 있는 6개의, 총 7개의 정육면체가 제거됩니다. 이 과정은 남은 20개의 작은 정육면체들에 반복됩니다.

An amazing cross-section inside the complement of the Menger sponge -iteration 5-.
멩거 스펀지(Menger sponge)의 정의: 정육면체는 3x3x3=27개의 동일한 작은 정육면체들로 잘립니다. 그 후 중심의 하나와 면의 중심에 있는 6개의, 총 7개의 정육면체가 제거됩니다. 이 과정은 남은 20개의 작은 정육면체들에 반복됩니다.
멩거 스펀지의 이 놀라운 단면은 다음 식으로 만들어 질 수 있습니다:
2X - 2Y + 2Z - 1 = 0
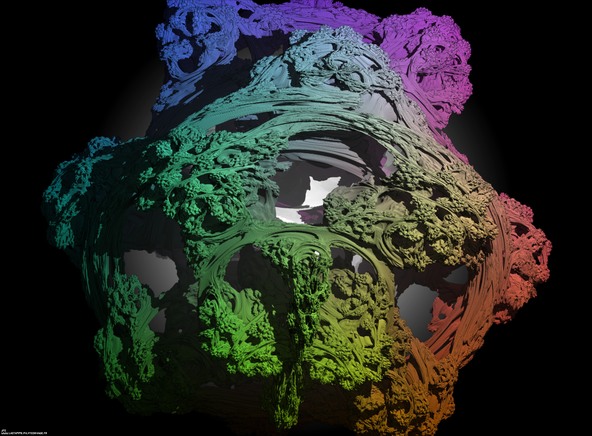
A foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.58...,+0.63...,0,0,0,0,0,0) with a rotation about the X axis -tridimensional cross-section-.
A foggy pseudo-octonionic Julia set computed with A=(-0.58...,+0.63...,0,0,0,0,0,0) with a rotation about the X axis -tridimensional cross-section-.

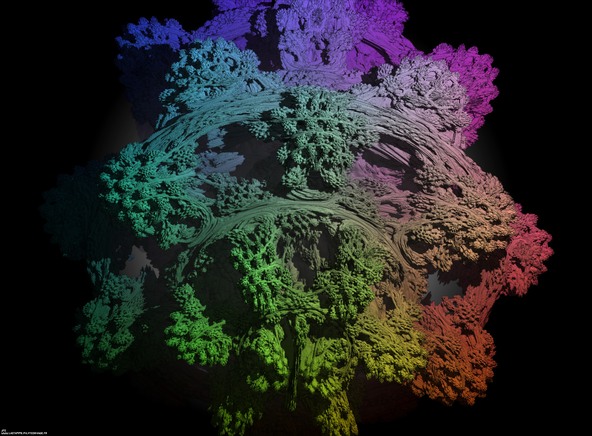
A foggy pseudo-octonionic Julia set computed with A=(-0.58...,+0.63...,0,0,0,0,0,0) with a rotation about the X axis -tridimensional cross-section-.

A foggy pseudo-octonionic Julia set computed with A=(-0.58...,+0.63...,0,0,0,0,0,0) -tridimensional cross-section-.

A foggy pseudo-octonionic Julia set computed with A=(-0.58...,+0.63...,0,0,0,0,0,0) -tridimensional cross-section-.
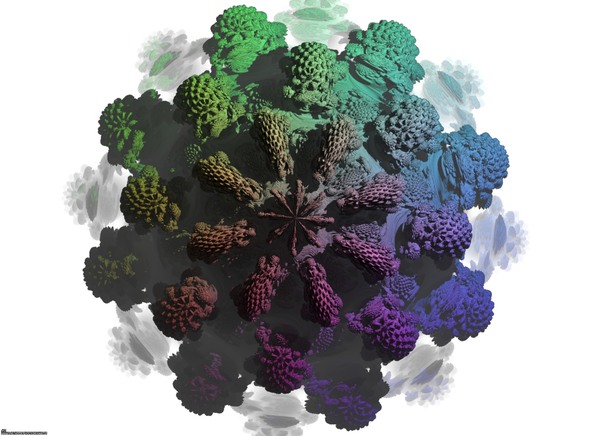
A foggy pseudo-octonionic Julia set computed with A=(-0.58...,+0.63...,0,0,0,0,0,0) -tridimensional cross-section-.



A tribute to Benoît Mandelbrot (1924-2010): tridimensional zoom in on the Mandelbrot set with mapping of the arguments.

Tridimensional visualization of the Verhulst dynamics
Verhulst 역학계는 다음 반복을 사용하여 정의됩니다.
X[0] = 0.5
X[n] = R.X[n-1].(1 - X[n-1])
여기 이 계산에서 증가율 ‘R’ 은 더 이상 일정하지 않지만 이것의 값은 아래 임의의 사이클을 따라 주기적으로 변화합니다.
R3 ==> R3 ==> R2 ==> R1 ==> R2 ==> R3 ==> R1 ==> R2 ==> R3 ==> R1 ==> R1 ==> R1
{ R1 , R2, R3 }은 각각 이하의 도메인 [ 2.936,3.413 ] × [ 3.500,3.850 ] × [ 3.000,4.000 ] 내부의 현재 위치의 세 좌표들입니다.
오직 음의 Lyapunov 지수를 갖는 동적 시스템에 해당하는 점들만 표시됩니다.

Tridimensional visualization of the Verhulst dynamics
Verhulst 역학계는 다음 반복을 사용하여 정의됩니다.
X[0] = 0.5
X[n] = R.X[n-1].(1 - X[n-1])
여기 이 계산에서 증가율 ‘R’ 은 더 이상 일정하지 않지만 이것의 값은 아래 임의의 사이클을 따라 주기적으로 변화합니다.
R3 ==> R3 ==> R2 ==> R1 ==> R2 ==> R3 ==> R1 ==> R2 ==> R3 ==> R1 ==> R1 ==> R1
{ R1 , R2, R3 }은 각각 이하의 도메인 [ 2.936,3.413 ] × [ 3.500,3.850 ] × [ 3.000,4.000 ] 내부의 현재 위치의 세 좌표들입니다.
오직 음의 Lyapunov 지수를 갖는 동적 시스템에 해당하는 점들만 표시됩니다.

Tridimensional visualization of the Verhulst dynamics
Verhulst 역학계는 다음 반복을 사용하여 정의됩니다.
X[0] = 0.5
X[n] = R.X[n-1].(1 - X[n-1])
여기 이 계산에서 증가율 ‘R’ 은 더 이상 일정하지 않지만 이것의 값은 아래 임의의 사이클을 따라 주기적으로 변화합니다.
R3 ==> R3 ==> R2 ==> R1 ==> R2 ==> R3 ==> R1 ==> R2 ==> R3 ==> R1 ==> R1 ==> R1
{ R1 , R2, R3 }은 각각 이하의 도메인 [ 2.936,3.413 ] × [ 3.500,3.850 ] × [ 3.000,4.000 ] 내부의 현재 위치의 세 좌표들입니다.
오직 음의 Lyapunov 지수를 갖는 동적 시스템에 해당하는 점들만 표시됩니다.

Tridimensional visualization of the Verhulst dynamics
Verhulst 역학계의 삼차원 시각화
Verhulst 역학계는 다음 반복을 사용하여 정의됩니다.
X[0] = 0.5
X[n] = R.X[n-1].(1 - X[n-1])
여기 이 계산에서 증가율 ‘R’ 은 더 이상 일정하지 않지만 이것의 값은 아래 임의의 사이클을 따라 주기적으로 변화합니다.
R3 ==> R3 ==> R2 ==> R1 ==> R2 ==> R3 ==> R1 ==> R2 ==> R3 ==> R1 ==> R1 ==> R1
{ R1 , R2, R3 }은 각각 이하의 도메인 [ 2.936,3.413 ] × [ 3.500,3.850 ] × [ 3.000,4.000 ] 내부의 현재 위치의 세 좌표들입니다.
오직 음의 Lyapunov 지수를 갖는 동적 시스템에 해당하는 점들만 표시됩니다.

Tridimensional visualization of the Verhulst dynamics
Verhulst 역학계는 다음 반복을 사용하여 정의됩니다.
X[0] = 0.5
X[n] = R.X[n-1].(1 - X[n-1])
여기 이 계산에서 증가율 ‘R’ 은 더 이상 일정하지 않지만 이것의 값은 아래 임의의 사이클을 따라 주기적으로 변화합니다.
R3 ==> R3 ==> R2 ==> R1 ==> R2 ==> R3 ==> R1 ==> R2 ==> R3 ==> R1 ==> R1 ==> R1
{ R1 , R2, R3 }은 각각 이하의 도메인 [ 2.936,3.413 ] × [ 3.500,3.850 ] × [ 3.000,4.000 ] 내부의 현재 위치의 세 좌표들입니다.
오직 음의 Lyapunov 지수를 갖는 동적 시스템에 해당하는 점들만 표시됩니다.

Tridimensional visualization of the Verhulst dynamics
Verhulst 역학계는 다음 반복을 사용하여 정의됩니다.
X[0] = 0.5
X[n] = R.X[n-1].(1 - X[n-1])
여기 이 계산에서 증가율 ‘R’ 은 더 이상 일정하지 않지만 이것의 값은 아래 임의의 사이클을 따라 주기적으로 변화합니다.
R1 ==> R2 ==> R3 ==> R1 ==> R1 ==> R2 ==> R2 ==> R3 ==> R3 ==> R1 ==> R1 ==> R1 ==> R2 ==> R2 ==> R2 ==> R3 ==> R3 ==> R3 ==> R1 ==> R1 ==> R1 ==> R1 ==> R2 ==> R2 ==> R2 ==> R2 ==> R3 ==> R3 ==> R3 ==> R3
{ R1 , R2, R3 }은 각각 이하의 도메인 [ 2.936,3.413 ] × [ 3.500,3.850 ] × [ 3.000,4.000 ] 내부의 현재 위치의 세 좌표들입니다.
오직 음의 Lyapunov 지수를 갖는 동적 시스템에 해당하는 점들만 표시됩니다.

Tridimensional visualization of the Verhulst dynamics
Verhulst 역학계는 다음 반복을 사용하여 정의됩니다.
X[0] = 0.5
X[n] = R.X[n-1].(1 - X[n-1])
여기 이 계산에서 증가율 ‘R’ 은 더 이상 일정하지 않지만 이것의 값은 아래 임의의 사이클을 따라 주기적으로 변화합니다.
R1 ==> R2 ==> R3 ==> R1 ==> R1 ==> R2 ==> R2 ==> R3 ==> R3 ==> R1 ==> R1 ==> R1 ==> R2 ==> R2 ==> R2 ==> R3 ==> R3 ==> R3 ==> R1 ==> R1 ==> R1 ==> R1 ==> R2 ==> R2 ==> R2 ==> R2 ==> R3 ==> R3 ==> R3 ==> R3
{ R1 , R2, R3 }은 각각 이하의 도메인 [3.212,3.370]x[3.500,3.616]x[3.000,4.000] 내부의 현재 위치의 세 좌표들입니다. 오직 음의 Lyapunov 지수를 갖는 동적 시스템에 해당하는 점들만 표시됩니다.
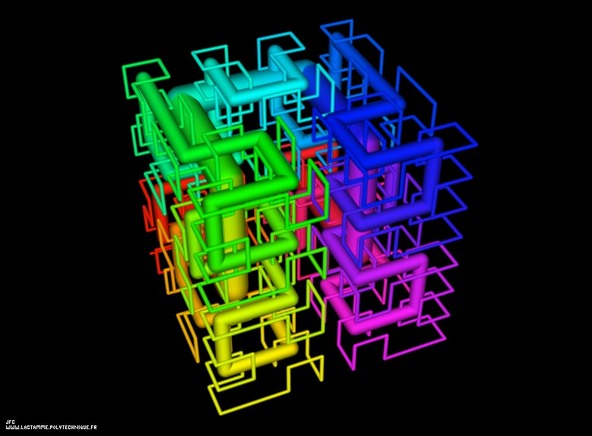



Tridimensional view of the first four iterations of the construction of the von Koch snowflake
(제목번역: 코흐 곡선의 첫 4단계 반복의 3차원 조망)

The first four iterations of the construction of the von Koch snowflake
(제목번역: 코흐 곡선의 첫 4단계 반복)





























































































