The Universum is the science museum of the UNAM (Universidad Nacional Autónoma de México). On December 8, 2017 it inaugurated the “Imaginario matemático”, a permanent exhibition which connects mathematical concepts with art, interactive installations and images. It features a variety of topics, from prime numbers to knot theory, from polyhedra to tesselations. IMAGINARY is part of this new space, with a big SURFER interactive exhibit!
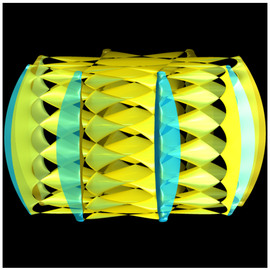
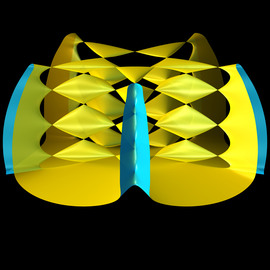
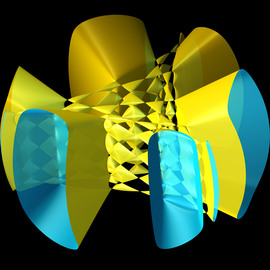
Nudos Salvajes
Los nudos matemáticos se estudian en la topología y se clasifican en dos: los mansos y los salvajes. Los nudos mansos son los que se pueden construir con una cuerda en la vida real. Los nudos salvajes son los que no.

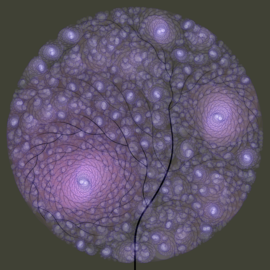
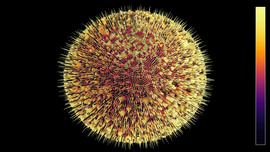
Nudos Salvaje (detalle)
Los nudos matemáticos se estudian en la topología y se clasifican en dos: los mansos y los salvajes. Los nudos mansos son los que se pueden construir con una cuerda en la vida real. Los nudos salvajes son los que no. En esta imagen podemos observar un pedazo de un nudo salvaje. Este está construido a partir de un collar, anudado, de esferas reflejantes; y en realidad, corresponde a la curva que está contenida en las sucesivas imágenes del collar en cada una de las esferas, iterativamente. Este curva tiene, además, naturaleza fractal.