The National Institute for Mathematical Sciences (NIMS) presents a very special NIMS-IMAGINARY exhibition in collaboration with the ICM committee and the Mathematisches Forschungsinstitut Oberwolfach (MFO). It will feature the best of all IMAGINARY modules of the last years and a lot of new software, images, films and sculptures. It will be the biggest IMAGINARY exhibition shown so far.
FroZenLight
program
[|||Desktop|||] Double click on the jar file or right click on it and select open with jre/jdk/java. Select museum from the menu for a touchscreen view. Or start it with java -jar frozenlight-1.2.2.jar -f -mu from the command line to get a touchscreen.If you are upgrading from version 1.1.1 delete the .frozenlight folder in your home directory before starting the 1.2.x version.
[|||Android|||] Go to Configuration->Security and allow installation from unknown sources. Tap on the frozenlight-0.1.1.apk file in your file manager to install the app.
Licenses
Source code
Website
Contributors
A project byZoltan Palmer
Related Events
The Heidelberg Laureate Forum Foundation invites you to visit the exhibition “Mathematics of Planet Earth” at Karlstorbahnhof in Heidelberg, Germany! It runs from July 5 to Aug 2, 2015, for the first time in Heidelberg. It offers a big variety of exciting adventures for children and adults alike.
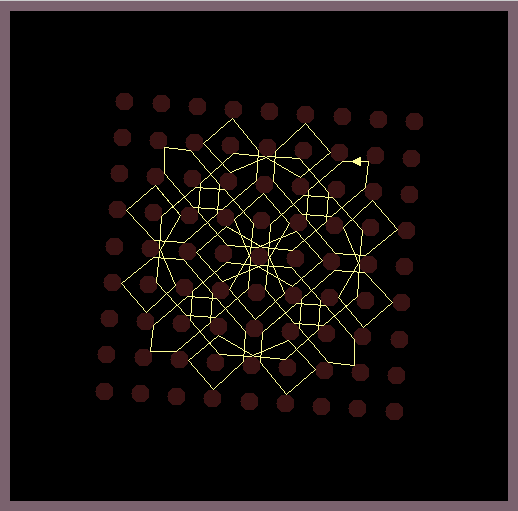
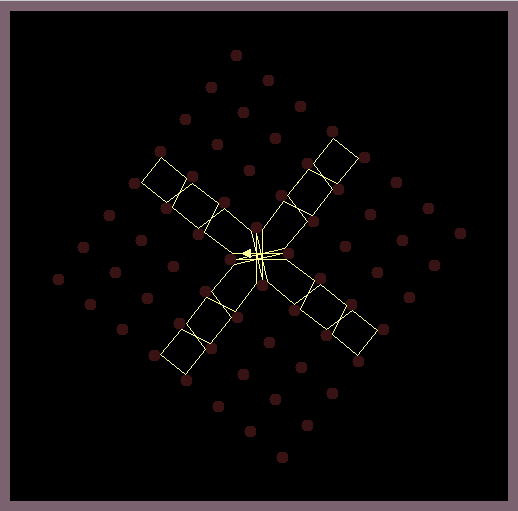
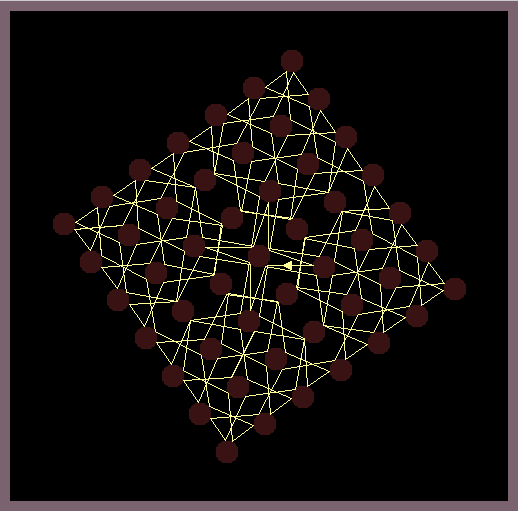
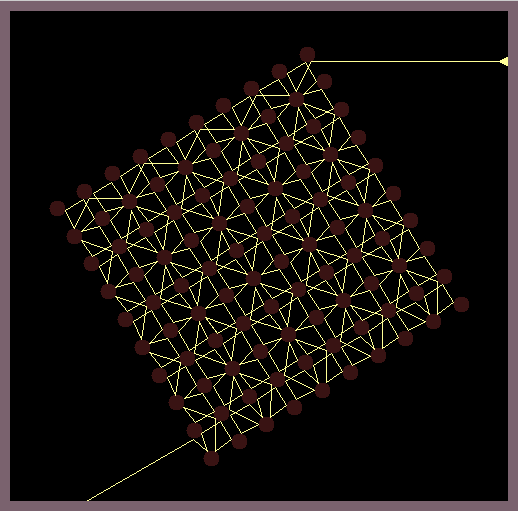
Circular shaped mirrors which are arranged in a grid-like manner reflect a light ray according to the reflection law of geometric optics. While random positions of the light source produce chaotic reflection patterns, it is possible to position the light source so that beautiful symmetric reflection patterns are created.
The application allows you to interactively change parameters like light source position, circle radius and rotation angle of the lattice. Through a simple menu it is possible to select and explore a wide range of symmetric reflection patterns.
Featured User Gallery
All images in this gallery are made with the open source software FroZenLight available at http://frozenlight. altervista.org
The software casts a light ray onto a grid of circular shaped mirrors and calculates all subsequent reflections by the law of geometric optics (the wave like nature of light is omitted). This simple model is very chaotic as errors of the position of the light source quickly blow up and indeed arbitrary precision math is needed to calculate most of reflection patterns.
The images in this gallery show symmetric reflection patterns emerging at special positions of the light source and special rotations of the mirroring lattice. Observe that the ray that leaves the light source (small triangle) enters the light source exactly at the same height on the backside.
The FroZenLight application is highly interactive and comes with a lot of predefined patterns.
FroZenLight - Ornament
FroZenLight - Cross
FroZenLight - Four Trees
FroZenLight - Cubistic Star
FroZenLight - Rock Crystals
FroZenLight - Patchwork
A main feature of the simple circle lattice model is that all reflection patterns depend sensibly on the given parameters meaning that the slightest change has a dramatic impact. Long numbers are therefore needed to reveal the intrinsic beauty of the model (see FroZenLight gallery).
Math exercises with solutions and further documentation are provided at the homepage.
