Free surfaces
This gallery contains visualizations of so-called free surfaces.
Freeness is an algebraic property, which is not so easy to explain: roughly, it means that a free surface has singular curves, which have a very “nice” algebraic structure (i. e., their defining ideal, the Jacobian ideal of the surface, is Cohen—Macaulay).
Free hypersurfaces were introduced 1980 by Kyoji Saito via logarithmic derivations and logarithmic differential forms. Since then there has been done a lot of research revealing interesting properties of free divisors and surprisingly free divisors pop up in quite different areas of mathematics, like deformation theory and combinatorics.
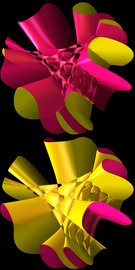
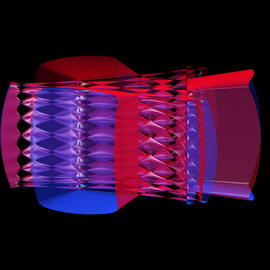
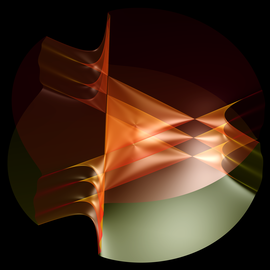
We start the gallery with the 17 so-called Sekiguchi free surfaces (named after Jiro Sekiguchi, who found them with a lot of computational effort).

Formül
- 16x^4z-4x^3y^2-128x^2z^2+144xy^2z-27y^4+256z^3
Fa_1 (aka Swallowtail)

Fa_2

Fb_1

Fb_2

Fb_3

Fb_4

Fb_5

Fb_6

Fb_7

Fh_1

Fh_2
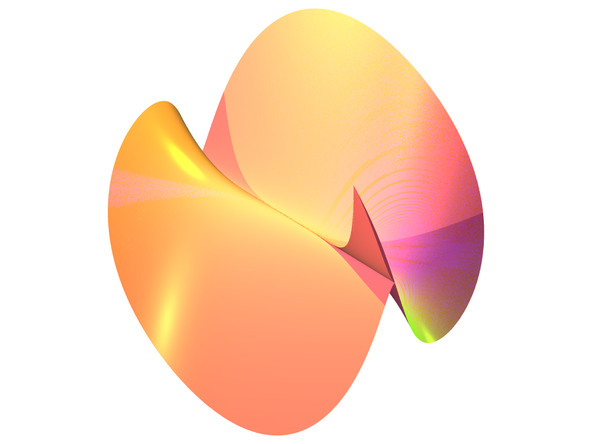
Fh_3

Fh_4

Fh_5

Fh_6