Free surfaces
갤러리
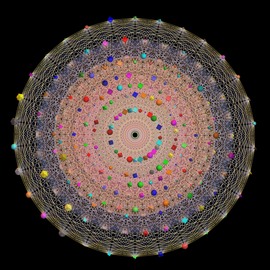
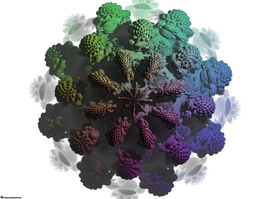
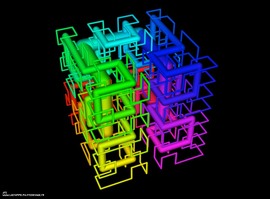
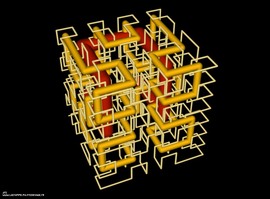
Free surfaces
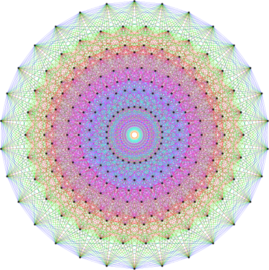
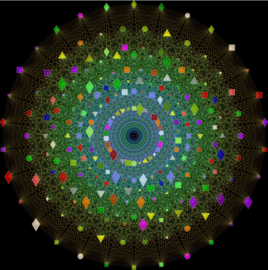
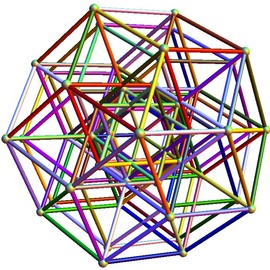
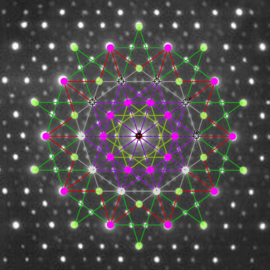
이 갤러리는 소위 말하는 자유곡면(free surface)을 시각화한 사진을 담고 있습니다.
자유성은 설명하기 힘든 대수적인 성질입니다. 대략적으로 자유곡면이 매우 ‘좋은’ 대수적 구조를 갖는 특이곡선(singular curve)을 갖는 것을 말합니다. (이를 정의하는 아이디얼, 즉, 그 곡면의 자코비안 아이디얼이 Cohen-Macaulay 임을 말합니다.)
자유 초곡면(hypersurface)들은 로그 미분, 로그 미분형식을 통해 1980년 쿄지 사이토(Kyoji Saito)에 의해 소개되었습니다. 그로부터 자유인자(free divisors)들의 흥미로운 성질을 밝히기 위한 많은 연구가 있었고, 놀랍게도 자유인자들은 변형이론(deformation theory)이나 조합론 같은 다른 수학분야에도 등장했습니다.
이 갤러리에는 17개의 세키구치 자유 곡면들이 포함되어 있습니다. (엄청난 계산을 통해서 이 곡면을 발견한 세키구치 지로(Jiro Sekiguchi)의 이름을 따 왔습니다).

공식
- 16x^4z-4x^3y^2-128x^2z^2+144xy^2z-27y^4+256z^3
Fa_1 (aka Swallowtail)
저작권 CC BY-NC-SA-3.0

Fa_2
저작권 CC BY-NC-SA-3.0

Fb_1
저작권 CC BY-NC-SA-3.0

Fb_2
저작권 CC BY-NC-SA-3.0

Fb_3
저작권 CC BY-NC-SA-3.0

Fb_4
저작권 CC BY-NC-SA-3.0

Fb_5
저작권 CC BY-NC-SA-3.0

Fb_6
저작권 CC BY-NC-SA-3.0

Fb_7
저작권 CC BY-NC-SA-3.0

Fh_1
저작권 CC BY-NC-SA-3.0

Fh_2
저작권 CC BY-NC-SA-3.0
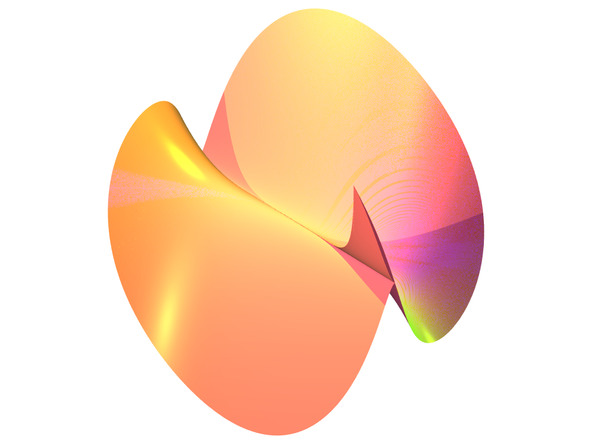
Fh_3
저작권 CC BY-NC-SA-3.0

Fh_4
저작권 CC BY-NC-SA-3.0

Fh_5
저작권 CC BY-NC-SA-3.0

Fh_6
저작권 CC BY-NC-SA-3.0

Fh_7
저작권 CC BY-NC-SA-3.0