Wizard Gynoid's Virtual E8 Polytope
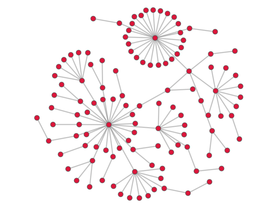
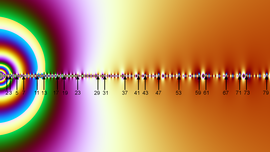
The E8 Polytope is an 8-dimensional object considered by mathematicians to be the most elegantly symmetrical and aesthetically pleasing geometric object known. Here we see 3D and 2D projections (shadows) of the 8D object. Of particular interest are the various symmetry axes, some of which display icosahedral, hexahedral and octahedral symmetries. The vertical symmetry axis resolves into the familiar concentric circles graph, with an unobstructed tunnel running through the complex object. An animated GIF is available for download beautifully demonstrating the various symmetry axes.

SXSW 2013 in Inworldz
The 3D and 2D “shadows” of the E8 Polytope on a sim in the virtual world of Inworldz. http;//inworldz.com The 200 meter diameter 3D projection is one linked and rotating object, comprised of almost 7,000 prims.

Journey to the Center of the E8 Polytope
This is the exact center of the E8 Polytope, looking down through the unobstructed tunnel to the 2D projection below.
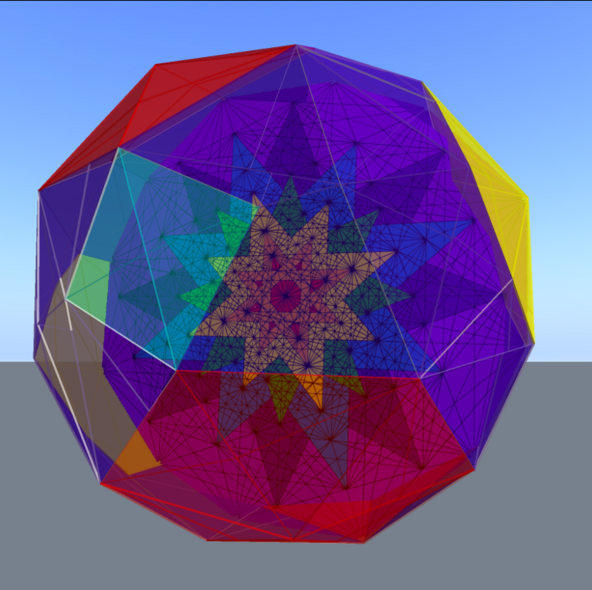
Wizardgynoiderene
Inspired to map a skin onto the surface of the 3D projection, I named the resulting polyhedron the Wizardgynoiderene. Inside we see a projection of the octahedral symmetry axis of the internal object.

Formül
- =F4 = (1/2) (1 + Sqrt[5]); =F9 = Exp[I Pi / 30]; a = Sqrt[(1/2) (1 + =F4^(3/2)/(3^(1/2) 5^(1/4)))]; b = Sqrt[(1/2) (1 + =F4^(-3/2)/(3^(1/2) 5^(1/4)))]; c = Sqrt[(1/2) (1 - =F4^(-3/2)/(3^(1/2) 5^(1/4)))]; d = Sqrt[(1/2) (1 - =F4^(3/2)/(3^(1/2) 5^(1/4)))]; ci[n_] := 2 Cos[n Pi/30]; r1 = a/ci[9]; r2 = b/ci[9]; r3 = c/ci[9]; r4 = d/ci[9]; r5 = a/ci[3]; r6 = b/ci[3]; r7 = c/ci[3]; r8 = d/ci[3]; Ac[n_] := {r1 =F9^(2 n), r4 =F9^(22 n), r6 =F9^(14 n + 1), r7 =F9^(26 n + 1) }; Bc[n_] := {r2 =F9^(2 n + 29), r3 =F9^(22 n + 19), -r8 =F9^(14 n + 24), -r5 =F9^(26 n + 18) }; Cc[n_] := {r3 =F9^(2 n + 29), -r2 =F9^(22 n + 19), r5 =F9^(14 n + 24), -r8 =F9^(26 n + 18) }; Dc[n_] := {r4 =F9^(2 n), -r1 =F9^(22 n), r7 =F9^(14 n + 1), -r6 =F9^(26 n= + 1) }; Ec[n_] := {r5 =F9^(2 n), r8 =F9^(22 n), -r2 =F9^(14 n + 1), -r3 =F9^(26 n= + 1) }; Fc[n_] := {r6 =F9^(2 n + 29), r7 =F9^(22 n + 19), r4 =F9^(14 n + 24), r1 =F9^(26 n + 18) }; Gc[n_] := {r7 =F9^(2 n + 29), -r6 =F9^(22 n + 19), -r1 =F9^(14 n + 24), r4 =F9^(26 n + 18) }; Hc[n_] := {r8 =F9^(2 n), -r5 =F9^(22 n), -r3 =F9^(14 n + 1), r2 =F9^(26 n= + 1) }; ptsA = Table[ Flatten[Table[{N[Re[Ac[n][[i]]]], N[Im[Ac[n][[i]]]]}, {i, 1, 4}]], {n, 0, 29}]; ptsB = Table[ Flatten[Table[{N[Re[Bc[n][[i]]]], N[Im[Bc[n][[i]]]]}, {i, 1, 4}]], {n, 0, 29}]; ptsC = Table[Flatten[Table[{N[Re[Cc[n][[i]]]], N[Im[Cc[n][[i]]]]}, {i, 1, 4}]], {n, 0, 29}]; ptsD = Table[Flatten[Table[{N[Re[Dc[n][[i]]]], N[Im[Dc[n][[i]]]]}, {i, 1, 4}]], {n, 0, 29}]; ptsE = Table[Flatten[Table[{N[Re[Ec[n][[i]]]], N[Im[Ec[n][[i]]]]}, {i, 1, 4}]], {n, 0, 29}]; ptsF = Table[Flatten[Table[{N[Re[Fc[n][[i]]]], N[Im[Fc[n][[i]]]]}, {i, 1, 4}]], {n, 0, 29}]; ptsG = Table[Flatten[Table[{N[Re[Gc[n][[i]]]], N[Im[Gc[n][[i]]]]}, {i, 1, 4}]], {n, 0, 29}]; ptsH = Table[Flatten[Table[{N[Re[Hc[n][[i]]]], N[Im[Hc[n][[i]]]]}, {i, 1, 4}]], {n, 0, 29}]; pts = Join[ptsA, ptsB, ptsC, ptsD, ptsE, ptsF, ptsG, ptsH];
A Symmetry Axis of the E8 Polytope
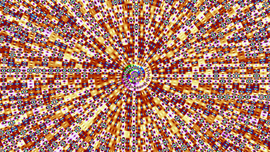
This is the octahedral symmetry axis, also shown in the preceding image.

3D & 2D Projections of the E8 Polytope with Polyhedron Skin
The colors of the external polyhedron skin identify the various symmetry axes. Yellow is icosahedral (5-fold), red is hexahedral (6-fold) and turquoise is octahedral (4-fold).

Octahedral Symmetry Axis of the E8 Polytope

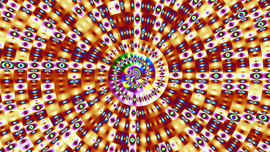
Double Spiral in the Octahedral Symmetry Axis of the E8 Polytope