Wizard Gynoid's Virtual E8 Polytope
갤러리
Wizard Gynoid's Virtual E8 Polytope
8차원 물체인 E8 폴리토프(polytope)는, 수학자들에게는 우아한 대칭성을 갖는 가장 아름다운 기하학적 대상으로 생각됩니다. 여기서 우리는 이 8차원 물체의 3차원, 2차원 투영(그림자)을 살펴봅니다. 우리의 관심사는 다양한 대칭축들으로, 이들의 일부는 종종 이십면체, 육면체, 팔면체의 대칭을 보여줍니다. 수직 대칭축은 이 복잡한 모형을 통과하는 뻥 뚫린 관을 갖는 친숙한 동심원 그래프로 분해합니다. 다양한 대칭축들을 보여주는 애니메이션 GIF 파일을 다운받을 수 있습니다.

SXSW 2013 in Inworldz
E8 폴리토프의 3차원 및 2차원의 그림자들을 Inworldz의 가상세계 sim에 그린 것입니다. (http://inworldz.com) 연결되고 회전하는 한 물체로 나타나는 지름 200미터의 3차원 사영은 거의 7000개의 prim들로 구성되어 있습니다.
저작권 CC BY-NC-SA-3.0

Journey to the Center of the E8 Polytope
뻥 뚫린 관을 통해 2차원 사영으로 밑을 내려다 보는 E8 폴리토프의 정중앙입니다.
저작권 CC BY-NC-SA-3.0
Wizardgynoiderene
3차원 사영 도형의 표면을 그려 넣는 아이디어로 만들어진 이 다면체를 저는 Wizardgynoiderene이라 명명했습니다. 안에서 우리는 팔면체의 대칭축의 사영을 볼 수 있습니다.
저작권 CC BY-NC-SA-3.0

공식
- =F4 = (1/2) (1 + Sqrt[5]); =F9 = Exp[I Pi / 30]; a = Sqrt[(1/2) (1 + =F4^(3/2)/(3^(1/2) 5^(1/4)))]; b = Sqrt[(1/2) (1 + =F4^(-3/2)/(3^(1/2) 5^(1/4)))]; c = Sqrt[(1/2) (1 - =F4^(-3/2)/(3^(1/2) 5^(1/4)))]; d = Sqrt[(1/2) (1 - =F4^(3/2)/(3^(1/2) 5^(1/4)))]; ci[n_] := 2 Cos[n Pi/30]; r1 = a/ci[9]; r2 = b/ci[9]; r3 = c/ci[9]; r4 = d/ci[9]; r5 = a/ci[3]; r6 = b/ci[3]; r7 = c/ci[3]; r8 = d/ci[3]; Ac[n_] := {r1 =F9^(2 n), r4 =F9^(22 n), r6 =F9^(14 n + 1), r7 =F9^(26 n + 1) }; Bc[n_] := {r2 =F9^(2 n + 29), r3 =F9^(22 n + 19), -r8 =F9^(14 n + 24), -r5 =F9^(26 n + 18) }; Cc[n_] := {r3 =F9^(2 n + 29), -r2 =F9^(22 n + 19), r5 =F9^(14 n + 24), -r8 =F9^(26 n + 18) }; Dc[n_] := {r4 =F9^(2 n), -r1 =F9^(22 n), r7 =F9^(14 n + 1), -r6 =F9^(26 n= + 1) }; Ec[n_] := {r5 =F9^(2 n), r8 =F9^(22 n), -r2 =F9^(14 n + 1), -r3 =F9^(26 n= + 1) }; Fc[n_] := {r6 =F9^(2 n + 29), r7 =F9^(22 n + 19), r4 =F9^(14 n + 24), r1 =F9^(26 n + 18) }; Gc[n_] := {r7 =F9^(2 n + 29), -r6 =F9^(22 n + 19), -r1 =F9^(14 n + 24), r4 =F9^(26 n + 18) }; Hc[n_] := {r8 =F9^(2 n), -r5 =F9^(22 n), -r3 =F9^(14 n + 1), r2 =F9^(26 n= + 1) }; ptsA = Table[ Flatten[Table[{N[Re[Ac[n][[i]]]], N[Im[Ac[n][[i]]]]}, {i, 1, 4}]], {n, 0, 29}]; ptsB = Table[ Flatten[Table[{N[Re[Bc[n][[i]]]], N[Im[Bc[n][[i]]]]}, {i, 1, 4}]], {n, 0, 29}]; ptsC = Table[Flatten[Table[{N[Re[Cc[n][[i]]]], N[Im[Cc[n][[i]]]]}, {i, 1, 4}]], {n, 0, 29}]; ptsD = Table[Flatten[Table[{N[Re[Dc[n][[i]]]], N[Im[Dc[n][[i]]]]}, {i, 1, 4}]], {n, 0, 29}]; ptsE = Table[Flatten[Table[{N[Re[Ec[n][[i]]]], N[Im[Ec[n][[i]]]]}, {i, 1, 4}]], {n, 0, 29}]; ptsF = Table[Flatten[Table[{N[Re[Fc[n][[i]]]], N[Im[Fc[n][[i]]]]}, {i, 1, 4}]], {n, 0, 29}]; ptsG = Table[Flatten[Table[{N[Re[Gc[n][[i]]]], N[Im[Gc[n][[i]]]]}, {i, 1, 4}]], {n, 0, 29}]; ptsH = Table[Flatten[Table[{N[Re[Hc[n][[i]]]], N[Im[Hc[n][[i]]]]}, {i, 1, 4}]], {n, 0, 29}]; pts = Join[ptsA, ptsB, ptsC, ptsD, ptsE, ptsF, ptsG, ptsH];

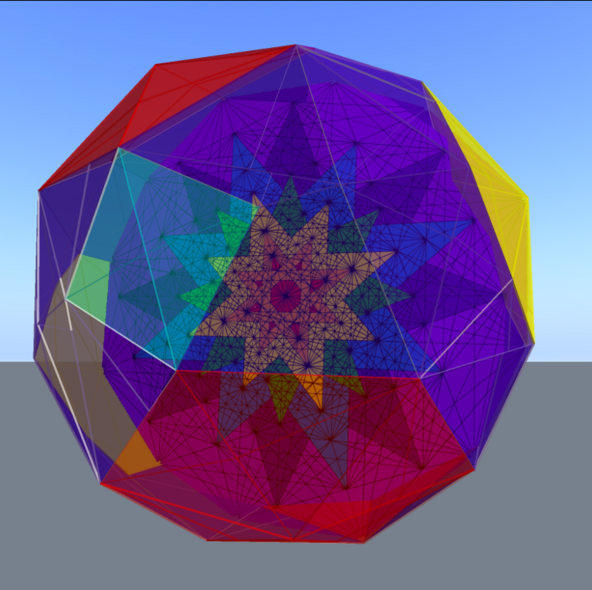
3D & 2D Projections of the E8 Polytope with Polyhedron Skin
바깥 다면체 표면의 색깔들은 다양한 대칭축들을 구분해줍니다. 노란색은 정20면체(5개), 빨간색은 정육면체(6개), 청록색은 정팔면체(4개)입니다.
저작권 CC BY-NC-SA-3.0

Octahedral Symmetry Axis of the E8 Polytope
저작권 CC BY-NC-SA-3.0

Double Spiral in the Octahedral Symmetry Axis of the E8 Polytope
저작권 CC BY-NC-SA-3.0

Single Spiral in the Octahedral Symmetry Axis of the E8 Polytope
저작권 CC BY-NC-SA-3.0





























































































