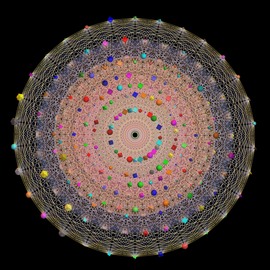
Cette surface de degré 6 (sextique) a été construite par Wolf Barth en 1996. Au total, elle a 65 singularités en tenant compte des 15 qui sont invisibles, situées à l’infini. Ce nombre de 65 est le nombre maximal de singularités d’une sextique, comme démontré en 1997 par Jaffe et Ruberman.

La construction de Barth fut une grande surprise: les géomètres crurent longtemps qu’une surface de degré 6 ne pouvait avoir plus de 64 singularités. La symétrie icosaédrale est l’une des caractéristiques frappantes de la sextique de Barth. Les sextiques à 65 singularités n’ont cependant pas toutes ce type de symétrie; il existe en fait une famille à 3 paramètres de surfaces à 65 singularités ! On peut choisir presque arbitrairement ces trois paramètres pour obtenir une telle surface. L’équation exacte de la sextique de Barth est P6 − αK2 = 0, où  P6 = ( τ2x2−y2)( τ2y2−z2)( τ2z2− x2),  τ= 1/2(1+√5) est le nombre d’or,  α = 1/4(2τ+1)=1/4(2+√5) et K = x2+y2+z2−1 décrit la sphère de rayon 1.

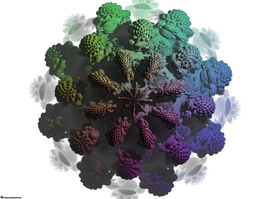
En 2004, alors qu’il rédige sa thèse de doctorat à Mayence, Oliver Labs construit une surface de degré 7 (septique) à 99 singularités. On sait depuis 1997 que le nombre maximum de singularités pour les surfaces de degré 6 est de 65. Pour le degré 7, un résultat de 1982 de A. N. Varchenko nous dit qu’il ne peut y avoir plus de 104 singularités. En 1992, Chmutov construit une septique à 93 singularités, établissant le record de l’époque. Après la construction de Labs, le record fut porté à 99. On ne sait toujours pas s’il existe des septiques à 100, 101, … , 104 singularités.

La septique de Labs a la symétrie d’un heptagone régulier. On peut cependant montrer qu’il existe une famille à 5 paramètres de septiques à 99 singularités, rappelant ainsi le résultat de Duco van Straten pour les sextiques. Pour construire la septique, Oliver Labs a utilisé le logiciel de calcul formel Singular, développé à l’université technique de Kaiserslautern. Ce logiciel est très bien adapté au travail avec les surfaces algébriques singulières.

Cette surface de degré 5 (quintique) a 15 singularités dont le type est appelé pli ou A2. La surface fait partie d’une série infinie de surfaces de degrés distincts construite par Oliver Labs en 2005. Comme on peut le voir sur l’image, 5 singularités se distinguent des autres. Elles sont plus précisément de type A2++ et les autres de type A2+-. Les premières sont localement décrites par l’équation x3+y2+z2 = 0, les autres par x3+y2-z2 = 0. L’équation de la quintique à 15 plis est S5(x, y)+t(z) = 0, où S5(x, y) = x5−10x3y2+5xy4−5x4−10x2y2− 5y4+20x2+20y2−16 est un pentagone régulier, et où le polynôme t(z) = −3z5+10z3−15z−8 est une variante des polynômes de Tchebychev. 

Équation de W. Barth (1995).
Visualisation : Oliver Labs

Équation de E. E. Kummer (années 1860).
Visualisation : Oliver Labs

Équation : classique (19è siècle), adaptée par Oliver Labs.
Visualisation : Oliver Labs