Jean-Francois Colonna - Number Theory
정수론의 그림들

The 126.646 first digits -base 6- of the square root of 2 displayed as a tridimensional random walk.
6진수의 각 숫자는 “절대적인” 3차원 브라운운동의 현재 위치를 정의합니다.
digit=0 ==> move(+D,0,0) digit=1 ==> move(-D,0,0) digit=2 ==> move(0,+D,0) digit=3 ==> move(0,-D,0) digit=4 ==> move(0,0,+D) digit=5 ==> move(0,0,-D)D=1
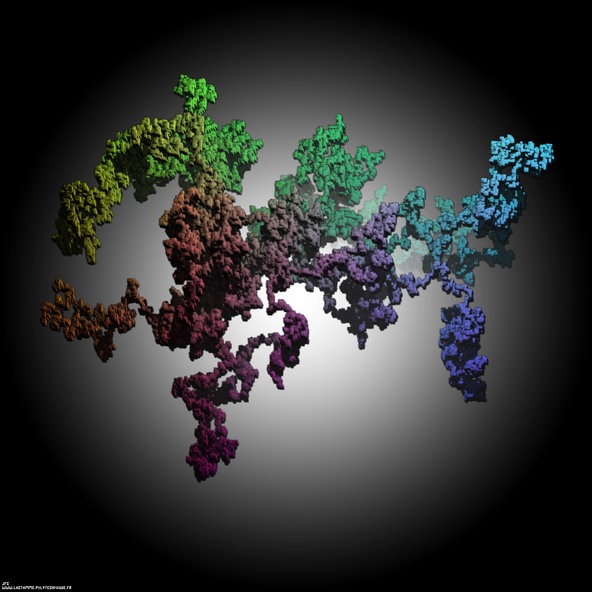
The 126.646 first digits -base 6- of the golden ratio displayed as a tridimensional random walk.
6진수의 각 숫자는 “절대적인” 3차원 브라운운동의 현재 위치를 정의합니다.
digit=0 ==> move(+D,0,0) digit=1 ==> move(-D,0,0) digit=2 ==> move(0,+D,0) digit=3 ==> move(0,-D,0) digit=4 ==> move(0,0,+D) digit=5 ==> move(0,0,-D)D=1
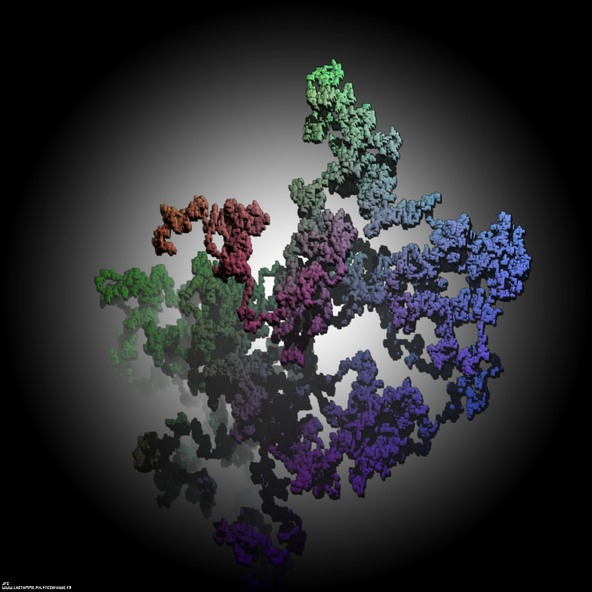
The 126.922 first digits -base 6- of 'e' displayed as a tridimensional random walk.
6진수의 각 숫자는 “절대적인” 3차원 브라운운동의 현재 위치를 정의합니다.
digit=0 ==> move(+D,0,0) digit=1 ==> move(-D,0,0) digit=2 ==> move(0,+D,0) digit=3 ==> move(0,-D,0) digit=4 ==> move(0,0,+D) digit=5 ==> move(0,0,-D)D=1

The 126.646 first digits -base 6- of 'pi' - displayed as a tridimensional random walk.
6진수의 각 숫자는 “절대적인” 3차원 브라운운동의 현재 위치를 정의합니다.
digit=0 ==> move(+D,0,0) digit=1 ==> move(-D,0,0) digit=2 ==> move(0,+D,0) digit=3 ==> move(0,-D,0) digit=4 ==> move(0,0,+D) digit=5 ==> move(0,0,-D)D=1
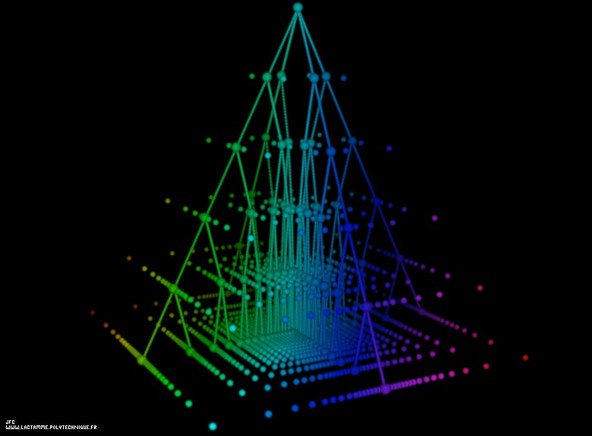
Generation of the 63x63 first Conway's surreal complex numbers

Tridimensional Hilbert Curve -iteration 4-.

A pseudo-periodical Penrose tiling of the Golden Decagon.
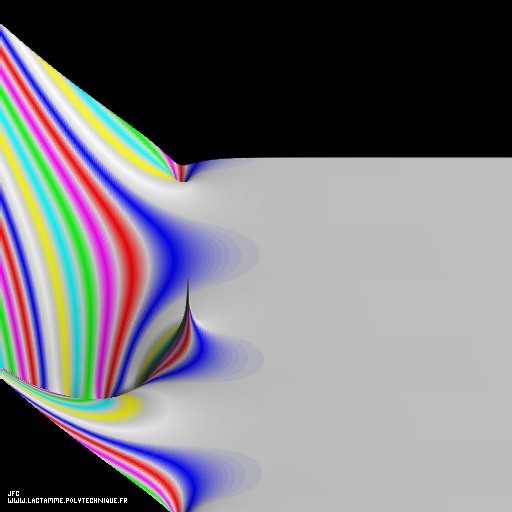
Tridimensional display of the Riemann Zeta function inside (-10.0,+20.0)x(-15.0,+15.0).

Tridimensional display of the Riemann Zeta function inside (+0.1,+0.9)x(0,+50).
아래는 3개의 좌표 {X,Y,Z}의 의미입니다.
X = Re(Zeta(z))Y = Im(Zeta(z))Z = Re(z)
The Goldbach conjecture -the Goldbach comet or the Goldbach rainbow- from 6 to 411678.
골드바흐의 추측이란 모든 4 이상의 짝수 N은 두 소수의 합으로 표현 가능하다느 것입니다. 예를 들어:
4 = 2+2 6 = 3+3 8 = 3+5 [= 5+3] 10 = 3+7 = 5+5 [= 7+3] (…) 70 = 3+67 = 11+59 = 17+53 = 23+47 = 29+41 [= 41+29 = 47+23 = 53+17 = 59+11 = 67+3] (…) 990 = 7+983 = 13+977 = 19+971 = 23+967 = 37+953 = 43+947 = 53+937 = 61+929 = 71+919 = 79+911 = 83+907 = 103+887 = 107+883 = 109+881 = 113+877 = 127+863 = 131+859 = 137+853 = 151+839 = 163+827 = 167+823 = 179+811 = 181+809 = 193+797 = 229+761 = 233+757 = 239+751 = 251+739 = 257+733 = 263+727 = 271+719 = 281+709 = 307+683 = 313+677 = 317+673 = 331+659 = 337+653 = 347+643 = 349+641 = 359+631 = 373+617 = 383+607 = 389+601 = 397+593 = 419+571 = 421+569 = 433+557 = 443+547 = 449+541 = 467+523 = 487+503 = 491+499 [= 499+491 = 503+487 = 523+467 = 541+449 = 547+443 = 557+433 = 569+421 = 571+419 = 593+397 = 601+389 = 607+383 = 617+373 = 631+359 = 641+349 = 643+347 = 653+337 = 659+331 = 673+317 = 677+313 = 683+307 = 709+281 = 719+271 = 727+263 = 733+257 = 739+251 = 751+239 = 757+233 = 761+229 = 797+193 = 809+181 = 811+179 = 823+167 = 827+163 = 839+151 = 853+137 = 859+131 = 863+127 = 877+113 = 881+109 = 883+107 = 887+103 = 907+83 = 911+79 = 919+71 = 929+61 = 937+53 = 947+43 = 953+37 = 967+23 = 971+19 = 977+13 = 983+7] (…)The horizontal axis represents the even numbers N={6, 8, 10, 12,…} starting at 6 (for compatibility with the other related visualizations). The “altitude” of each point exhibits the number of decompositions of N as sums of two prime numbers.
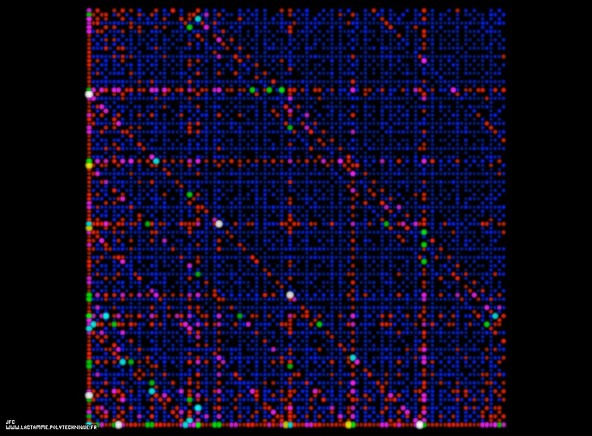
The ABC conjecture.
수평축과 수직축은 각각 두 수 A, B를 나타냅니다. 각각의 디스크는 서로소인 A, B, 즉 다음을 만족하는 (A, B)의 쌍을 나타냅니다.
GCD(A,B)=1C는 A와 B의 합입니다.
C = A+B함수 Radical(N)읜 N의 소인수들의 곱입니다. 예를 들어:
N = 1960 = 2^3 .5^1 .7^2 Radical(1960) = 2^1 .5^1 .7^1 = 2.5.7 = 70그러면 다음 함수가 계산됩니다.
k(A,B,C) = log(C) / log(Radical(A. B.C))ABC 추측은 A, B의 값에 관계없이 k(A,B,C)가 어떤 상수(알려지지 않았지만, 1보단 크고 2보단 작을 것 같은…)보다 작다는 것입니다.
표면과 각 디스크의 밝기는 k(A, B, C)의 비율입니다.
이 그림에서 [1, 100] 구간에 있는 A와 B의 값은 다음 값들을 줍니다.
min(k(A,B,C))=0.37117806024788 max(k(A,B,C))=1.22629438553090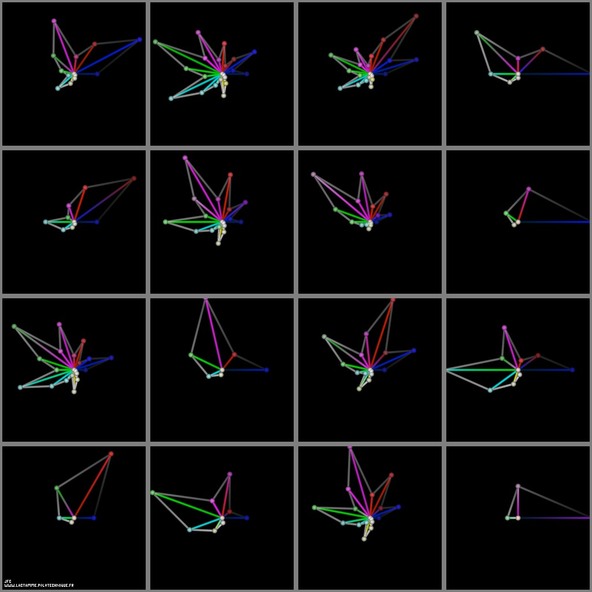
The Syracuse conjecture -polar coordinates display-
Syracuse수열은 다음과 같이 정의됩니다:
U(0) = N (정수)U(n)이 짝수이면 :
U(n+1) = U(n)/2
아니면 :
U(n+1) = 3.U(n) + 1
- Syracuse 추측은 시작하는 수 N이 무엇이던간에 {[[4,] 2,] 1}수열이 언젠가 등장한다는 것입니다.(그러고 위의 식을 반복). 예를 들어 N이 7이면:
U(0) = 7 U(1) = 22 U(2) = 11 U(3) = 34 U(4) = 17 U(5) = 52 U(6) = 26 U(7) = 13 U(8) = 40 U(9) = 20 U(10) = 10 U(11) = 5 U(12) = 16 U(13) = 8 U(14) = 4 U(15) = 2 U(16) = 1
- 이 그림은 U(0)=5로 시작하여 U(0)=20 로 끝나는 16개의 다른 수열을 원형으로 나타내었습니다. 각 수열 U(n) 은 아래의 “별”이 만들어냅니다:
Rho(n) = U(n) (with a renormalization inside [0,1])Teta(n) = 2.pi.n/(nm+1)X(n) = Rho(n).cos(Teta(n)) Y(n) = Rho(n).sin(Teta(n))where ‘nm’ denotes the maximal value of ‘n’:
U(nm) = 1사용된 색들은 ‘n’의 함수입니다. (어두운 파란색 [n=0] 부터 증가하는 밝기의 흰색으로)

The additive persistence of the 65536 first integer numbers for the bases 2 -lower left- to 17 -upper right-.
좌표의 원점(사진의 중심)으로부터 시작하여, 사각형의 나선형 같은 길
을 따라가고 각 정수점들의 숫자들과 만나게 됩니다(1, 2, 3,…).
그리고 N번째 점을 다른 색깔 f(PA(N,B))로 다음과 같이 표현합니다:
PA(N,B) = N의 B진법 표현의 “additive persistence” (하단 예 참고) f(…) = 임의의 증가함수PA(N,B)는 다음 예시처럼 계산합니다.
B = 10 N = 856 (= 8xB^2 + 5xB^1 + 6xB^0)그러면 다음 수열이 계산됩니다.
856 —-> (8+5+6) = 19 —-> (1+9) = 10 —-> (1+0) = 1한 자리수에 이르기까지 3번의 과정이 걸리므로 따라서PA(856,10) = 3

The multiplicative persistence of the 65536 first integer numbers for the bases 2 -lower left- to 17 -upper right-.
좌표의 원점(사진의 중심)으로부터 시작하여, 사각형의 나선형 같은 길
을 따라가고 각 정수점들의 숫자들과 만나게 됩니다(1, 2, 3,…).
그리고 N번째 점을 다른 색깔 f(PM(N,B))로 다음과 같이 표현합니다:
Then one displays the N-th point with the false color f(PM(N,B)) where:
PM(N,B) = N의 B진법 표현의 “multiplicative persistence” (하단 예 참고)f(…) = 임의의 증가함수PM(N,B)는 다음 예시처럼 계산합니다.
B = 10 N = 77 (= 7xB^1 + 7xB^0)그러면 다음 수열이 계산됩니다.
77 —-> (7x7) = 49 —-> (4x9) = 36 —-> (3x6) = 18 —-> (1x8) = 8한 자리수에 이르기까지 4번의 과정이 걸리므로 따라서 (참고로 두 자리수 가운데서는 가장 오래 걸리는 과정입니다)PM(77,10) = 4 PM(N,10)은 11을 넘을 수 없다는 가설이 있습니다. 더 긴 수열의 예시는:48699984 —-> 4478976 —-> 338688 —-> 27648 —-> 2688 —-> 768 —-> 336 —-> 54 —-> 20 —-> 0
12 evenly distributed points on a sphere -an Icosahedron- by means of simulated annealing.
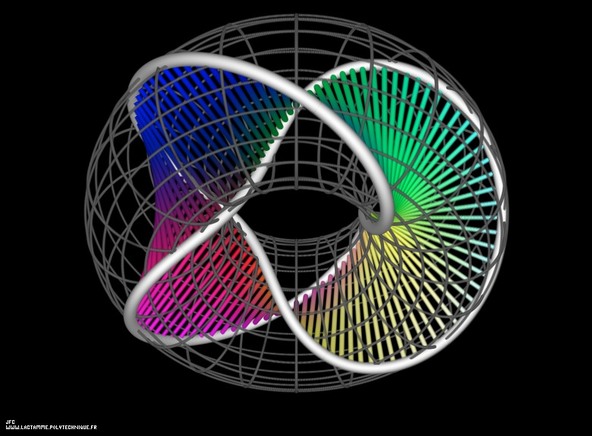
3-foil torus knot on its torus.

Three successive elementary monodimensional binary cellular automata -106,90,86- with 1 yellow starting point -bottom middle-.
1차원 이진수 자동자(automaton)는 1차원 세포들의 집합입니다. 시간 ‘t’에서 각각의 세포(좌표 ‘x’로 표현)는 ‘CELL(x,t)’라는 0(검은색) 혹은 1(하얀색)의 값을 가지고, 2개의 이웃 (하나는 왼쪽에 있는 ‘CELL(x-1,t)’고 하나는 오른쪽에 있는 ‘CELL(x+1,t)’)을 가집니다. 그림 밖에 있는 점들(왼쪽과 오른쪽에 있는 점들)은 흰색으로 가정합니다. 이 세포들의 집합의 시간변화는 몇 개의 규칙으로 정해집니다.
이 사진은 다음 3가지 기초적인 1차원의 2진수 세포 자동화를 사용하여 순차적으로 계산되었습니다.
automaton 86 (for t E [401,574]) -흰 배경-
automaton 90 (for t E [101,400]) -밝은 주황 배경-
automaton 106 (for t E [0,100]) -어두운 주황 배경-
수직 축은 시간 축이고 초기조건은 아래 선에 나타나 있습니다.

Tridimensional display of the dynamics of the bidimensional John Conway's life game
3번째 축 ‘Z’는 시간 ’T’이고, 두 공간 축 ‘X’와 ‘Y’는 주기적입니다

The tridimensional John Conway's life game with random initial conditions -25% of occupied cells-.
2차원 생명게임은 Conway에 의해 정의되었습니다. 그 게임은 비어있는 사각형 격자망을 사용합니다(모든 꼭지점은 꺼져있습니다). 시간 t=0일 때 몇 꼭지점들이 채워지고(켜지고), 이것이 초기 상태가 됩니다. 시간 t에서 t+1으로 갈 때는 각 꼭지점이나 “셀”-C(x, y)의 그 이웃의 숫자 N(3^2-1=8이하이다)을 세면 충분하고, 그러면 아래의 2차원 오토마타 규칙에 따라서 M의 상태를 바꿀 수 있습니다.
[R1 = Birth] ((C(t).IS.off).AND.(N == 3)) ==> C(t+1) on [R2 = Death] ((C(t).IS.on).AND.((N < 2).OR.(N > 3))) ==> C(t+1) off [R3] other cases ==> C(t+1)=C(t)경계조건들은 주기적이거나 아닐 수 있습니다.
이 과정은 3차원으로 확장될 수 있습니다. 꼭지점이나 “세포”-C(x, y, z)의 이웃 숫자 N이 비슷하게 계산되고(3^3-1=26 이하), 앞의 규칙이 다음과 같이 확장될 수 있습니다.
[R1 = Birth] ((C(t).IS.off).AND.((N >= NB1).AND.(N <= NB2))) ==> C(t+1) on [R2 = Death] ((C(t).IS.on).AND.((N < ND1).OR.(N > ND2))) ==> C(t+1) off [R3] other cases ==> C(t+1)=C(t)2차원과 3차원 과정은 두 2진수 ‘LD’와 ‘LA’ (각각 “Dead” -off- 와 “Alive” -on-)를 사용하면 한 단계 더 확장될 수 있습니다.
[R1 = Birth] ((C(t).IS.off).AND.(LD[N] == 1)) ==>C(t+1)=on [R2 = Death] ((C(t).IS.on).AND.(LA[N] == 1)) ==>C(t+1)=off [R3] other cases ==> C(t+1)=C(t)(“1”은 “상태 변화”를 의미하고 “0”은 “상태 불변”을 의미).
이 사진에서, 변수들은 아래의 값과 같습니다:
NB1=10 NB2=14 ND1=8 ND2=16
Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb') with a 1/O conformal transformation in the pseudo-octonionic space -tridimensional cross-section-.

Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb') with a 1/O conformal transformation in the pseudo-octonionic space -tridimensional cross-section-.

The 64 first lines of the Pascal's Triangle.
하얀색 뾰족점들은 2, 3, 5, 7로 나누어지는 계수들을 보여줍니다(2, 3, 5, 7로 안나눠지는 계수들은 어두운 파란색입니다). 다른색들은 다른 경우로 보여집니다. 각 점의 높이는 각 색의 밝기와 비례한다.
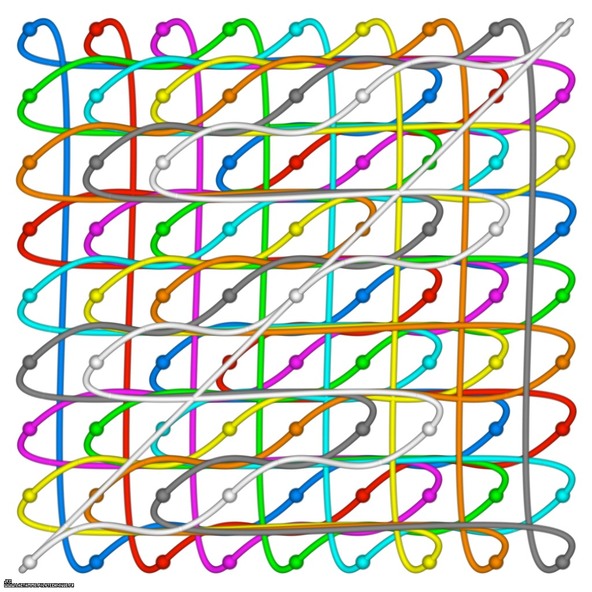
Artistic display of a Sudoku grid.
여기는 각 숫자(1부터 9)별로 각각의 색으로 표현된 격자가 사용되었습니다.
1 2 3 | 4 5 6 | 7 8 9 4 5 6 | 7 8 9 | 1 2 3 7 8 9 | 1 2 3 | 4 5 6 ———+———-+——— 2 3 4 | 5 6 7 | 8 9 1 5 6 7 | 8 9 1 | 2 3 4 8 9 1 | 2 3 4 | 5 6 7 ———+———-+——— 3 4 5 | 6 7 8 | 9 1 2 6 7 8 | 9 1 2 | 3 4 5 9 1 2 | 3 4 5 | 6 7 8























