Doyle Spirals Variations
gallery
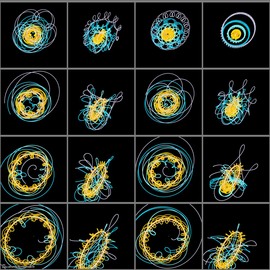
Doyle Spirals Variations
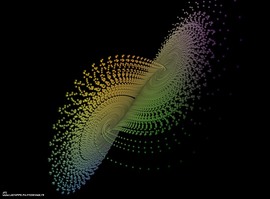
Doyle Spirals are a particular case of circle packing: each circle is surrounded with 6 tangent circles. When the parameters are well chosen (and this is the hard stuff), this circle packing can tile the plane. Applying to this tiling geometric transformations preserving the tangency property, one can create elegant patterns. This work was initiated while looking at the beautiful and challenging images created by Jos Leys.
Stone Spirals
Licence CC BY-NC-SA-3.0

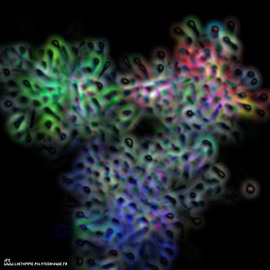
The World in a Nutshell
Through a circle inversion, all the circles tiling the plane are gathered inside one unique circle (not visible in this picture) : can you guess its color ?
Licence CC BY-NC-SA-3.0

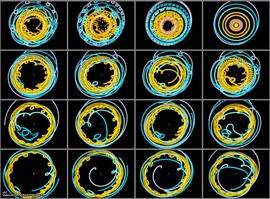
Inside the Riemann Sphere
Recipe : send the tiling on the surface on a sphere (ok, tangency is no more guaranted !), then go inside the sphere. Use highly reflective elementary spheres.
Licence CC BY-NC-SA-3.0

Licence CC BY-NC-SA-3.0

Licence CC BY-NC-SA-3.0