Wave equation
Simulations of the linear, hyperbolic wave equation on various domains, obtained by a finite difference scheme.


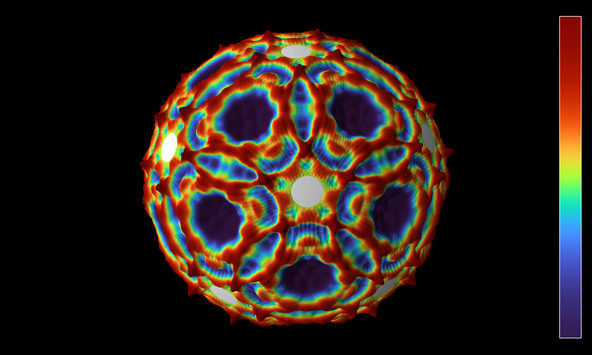
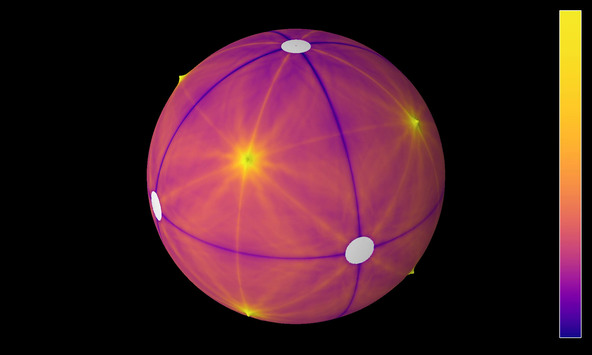
Waves with dodecahedral symmetry on a sphere
Solution of the wave equation on a sphere. Reflecting discs have been placed around the vertices of a regular dodecahedron. The initial state is a set of circular waves concentrated at the centers of the faces of the dodecahedron. The image shows the wave height.


Average energy of waves with dodecahedral symmetry on a sphere
Solution of the wave equation on a sphere. Reflecting discs have been placed around the vertices of a regular dodecahedron. The initial state is a set of circular waves concentrated at the centers of the faces of the dodecahedron. The image shows the energy of the wave, averaged over time.


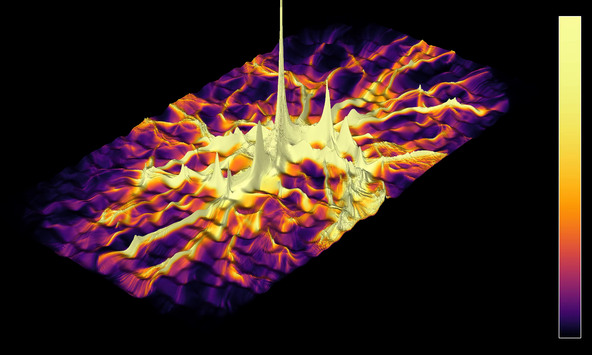
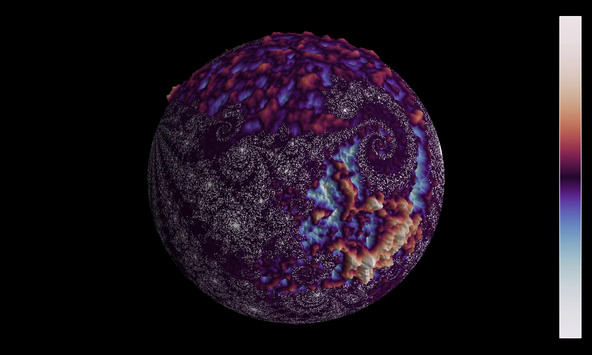
Average energy of a branched flow
Time-averaged energy of a solution to the wave equation in a random environment


Waves with icosahedral symmetry on the sphere
Solution of the wave equation on a sphere. Reflecting discs have been placed around the vertices of a regular icosahedron. The initial state is a set of circular waves concentrated at the centers of the faces of the icosahedron. The image shows the wave height.


Average energy of waves with icosahedral symmetry on the sphere
Solution of the wave equation on a sphere. Reflecting discs have been placed around the vertices of a regular icosahedron. The initial state is a set of circular waves concentrated at the centers of the faces of the icosahedron. The image shows the wave energy, averaged over a time interval.


Energy flux of waves with dodecahedral symmetry on a sphere
Solution of the wave equation on a sphere. Reflecting discs have been placed around the vertices of a regular dodecahedron. The initial state is a set of circular waves concentrated at the centers of the faces of the dodecahedron. The image shows the energy flux: radial coordinate and luminosity depend on the norm of the flux, and color hue depends on its direction.


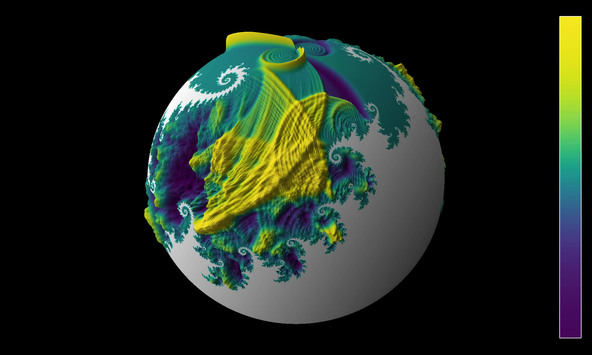
Waves in a Julia set on the Riemann sphere
A solution of the wave equation in a domain on the Riemann sphere, which is given by an approximation of a Julia set with parameter 0.37468 + 0.21115 i. The initial state is given by two circular waves, with opposite longitudes and positive latitude, and opposite sign. The colors and radial coordinate show the wave height.


Waves in a Julia set on the Riemann sphere
A solution of the wave equation in a domain on the Riemann sphere, which is given by an approximation of a Julia set with parameter 0.37468 + 0.21115 i. The initial state is given by two circular waves, with opposite longitudes and positive latitude, and opposite sign. The colors and radial coordinate show the energy averaged over a time interval.


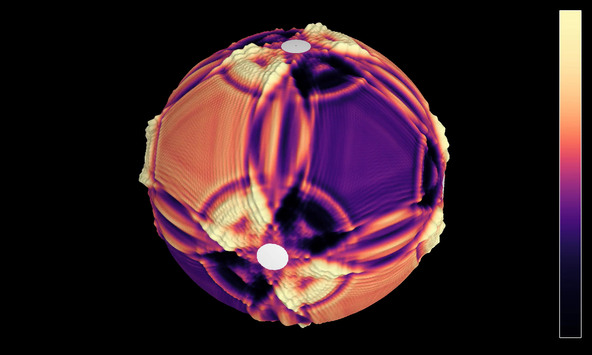
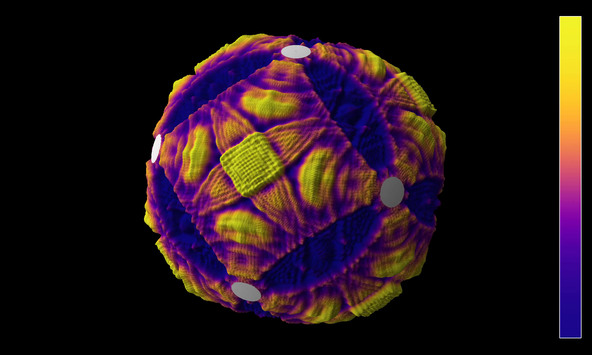
Waves with octahedral symmetry on the sphere
Solution of the wave equation on a sphere. Reflecting discs have been placed around the vertices of a regular octahedron. The initial state is a set of circular waves concentrated at the centers of the faces of the octahedron. The image shows the wave height.


Average energy of waves with octahedral symmetry on the sphere
Solution of the wave equation on a sphere. Reflecting discs have been placed around the vertices of a regular octahedron. The initial state is a set of circular waves concentrated at the centers of the faces of the octahedron. The image shows the wave energy averaged over a time interval.


Waves outside a disconnected Julia set on the Riemann sphere
A solution of the wave equation in a domain on the Riemann sphere, which is given by the complement of an approximation of a Julia set with parameter -0.77145 -0.10295 i. The initial state is given by two circular waves, with opposite longitudes and positive latitude, and opposite sign. The colors and radial coordinate show the energy averaged over a time interval.


Waves outside a disconnected Julia set on the Riemann sphere
A solution of the wave equation in a domain on the Riemann sphere, which is given by the complement of an approximation of a Julia set with parameter -0.77145 -0.10295 i. The initial state is given by two circular waves, with opposite longitudes and positive latitude, and opposite sign. The colors and radial coordinate show the wave height.


Waves in a Julia set on the Riemann sphere, equirectangular projection
A solution of the wave equation in a domain on the Riemann sphere, which is given by an approximation of a Julia set with parameter 0.37468 + 0.21115 i. The initial state is given by two circular waves, with opposite longitudes and positive latitude, and opposite sign. The image shows an equirectangular projection of the sphere.


Waves with cubic symmetry on the sphere
A solution of the wave equation on a sphere, obtained by a finite difference scheme. Reflecting obstacles of constant radius have been placed on the vertices of a cube. The initial state is a set of circular waves concentrated near the centers of the faces of the cube, which form a regular octahedron, and at the midpoints of the cube’s edges.


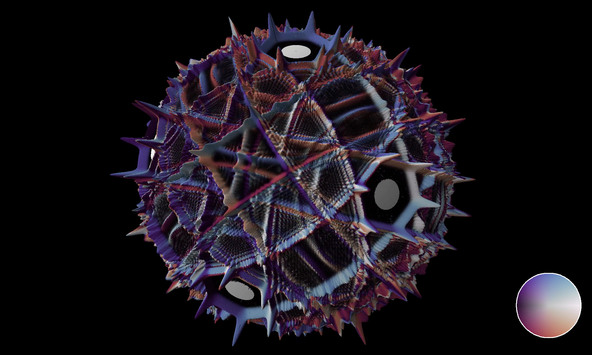
Energy flux of waves with cubic symmetry on the sphere
A solution of the wave equation on a sphere, obtained by a finite difference scheme. Reflecting obstacles of constant radius have been placed on the vertices of a cube. The initial state is a set of circular waves concentrated near the centers of the faces of the cube, which form a regular octahedron, and at the midpoints of the cube’s edges.The radial coordinate and luminosity depend on the intensity of the energy flux, while the color hue depends on its direction.


Waves with icosahedral symmetry on the sphere, 2d projection
Solution of the wave equation on a sphere. Reflecting discs have been placed around the vertices of a regular icosahedron. The initial state is a set of circular waves concentrated at the centers of the faces of the icosahedron. The image shows an equirectangular projection of the wave height.


Average energy of waves with icosahedral symmetry on the sphere, 2d projection
Solution of the wave equation on a sphere. Reflecting discs have been placed around the vertices of a regular icosahedron. The initial state is a set of circular waves concentrated at the centers of the faces of the icosahedron. The image shows an equirectangular projection of the wave energy averaged over a time interval.


Waves with dodecahedral symmetry on the sphere, 2d projection
Solution of the wave equation on a sphere. Reflecting discs have been placed around the vertices of a regular dodecahedron. The initial state is a set of circular waves concentrated at the centers of the faces of the dodecahedron. The image shows an equirectangular projection of the wave height.


Average energy of waves with dodecahedral symmetry on the sphere, 2d projection
Solution of the wave equation on a sphere. Reflecting discs have been placed around the vertices of a regular dodecahedron. The initial state is a set of circular waves concentrated at the centers of the faces of the dodecahedron. The image shows an equirectangular projection of the energy averaged over a time interval.


Waves with octahedral symmetry on the sphere, 2d projection
Solution of the wave equation on a sphere. Reflecting discs have been placed around the vertices of a regular octahedron. The initial state is a set of circular waves concentrated at the centers of the faces of the octahedron. The image shows an equirectangular projection of the energy averaged over a time interval.


Waves with cubic symmetry on the sphere, 2d projection
Solution of the wave equation on a sphere. Reflecting discs have been placed around the vertices of a cube. The initial state is a set of circular waves concentrated at the centers of the faces and edges of the cube. The image shows an equirectangular projection of the wave height.