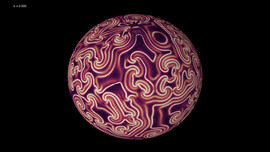
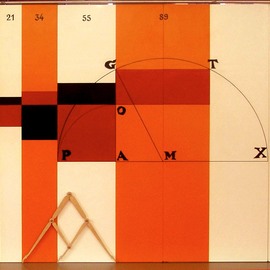
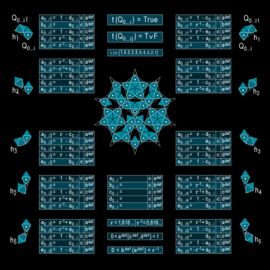
Turtle Geometry
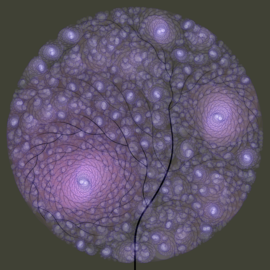
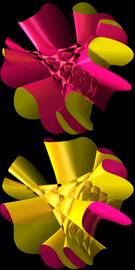
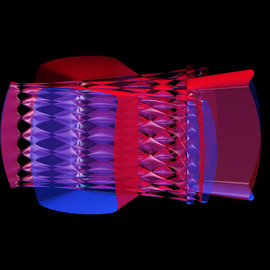
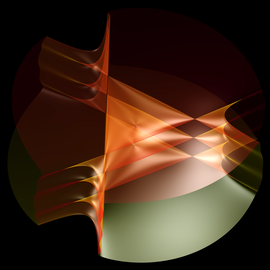
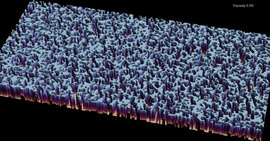
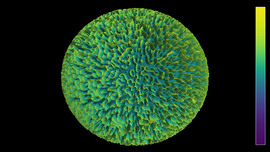
Turtle geometry is applied to create complex symmetric patterns. The change of inclination angles of lines follows some prescribed rules. Lines are combined with special functions to generate colorful surroundings.
Links to related videos:
https://youtu.be/cFmSeORtSbA
https://youtu.be/PVXQ_kgKDHg
https://youtu.be/6rDUGWSmxTk
https://youtu.be/0DQOnLm3BS4
https://youtu.be/iBBuF546wqM

Formula
- \varphi_{i+1} = \varphi_i + 170.5° \cdot i+180°
Turtle Object No 1
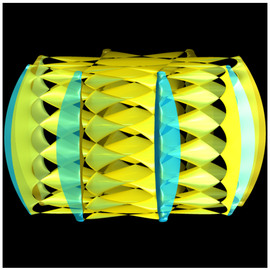
Formula
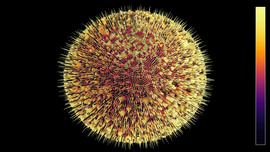
- \varphi_{i+1} = \varphi_i + 165.5° \cdot i+180°
Turtle Object No 2

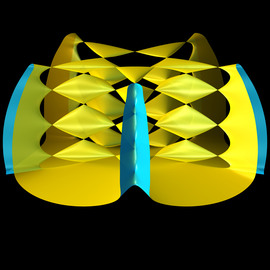
Formula
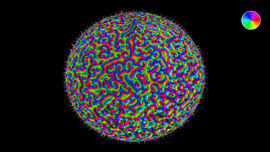
- \varphi_{i+1} = \varphi_i + 71.5° \cdot i+180°
Turtle Object No 3

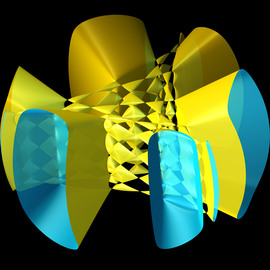
Formula
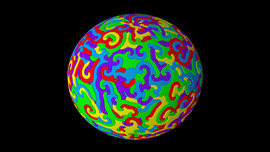
- \varphi_{i+1} = \varphi_i + 5.5° \cdot i+180°
Turtle Object No 4

Formula
- \varphi_{i+1} = \varphi_i + 60° \cdot i^2-180°
Turtle Object No 5

Formula
- \varphi_{i+1} = \varphi_i + 30° \cdot i^2-180°
Turtle Object No 6

Formula
- \varphi_{i+1} = \varphi_i + 150° \cdot i^2-180°
Turtle Object No 7

Formula
- \varphi_{i+1} = \varphi_i + 20° \cdot i^2-180°
Turtle Object No 8

Formula
- \varphi_{i+1} = \varphi_i + 40° \cdot i^2-180°
|
|
Turtle Object No 9
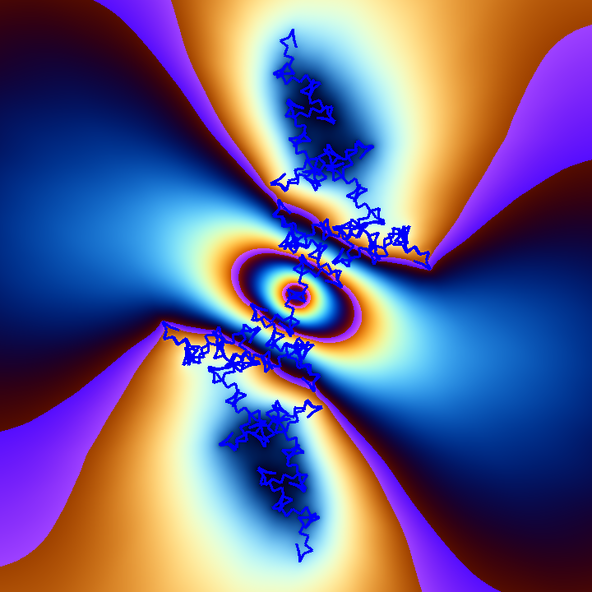
Turtle Geometry engages students in exploring mathematical properties visually via a simple programming language. This example shows a polygonal line consisting of a series of points connected by lines with unit length. The coordinates of each pointare calculated iteratively following simple rules.
The result is a beautiful figure with sixfold symmetry. By modification of the parameters interesting figures of different shape and symmetry are obtained.

Formula
- \varphi_{i+1} = \varphi_i + 100° \cdot i^2-180°
Turtle Object No 10

Formula
- \varphi_{i+1} = \varphi_i + 160° \cdot i^2-180°
Turtle Object No 11

Formula
- \varphi_{i+1} = \varphi_i + 15° \cdot i^2-180°
Turtle Object No 12

Formula
- \varphi_{i+1} = \varphi_i + 75° \cdot i^2-180°
Turtle Object No 13

Formula
- \varphi_{i+1} = \varphi_i + 105° \cdot i^2-180°
Turtle Object No 14

Formula
- \varphi_{i+1} = \varphi_i + 90°/7 \cdot i^2-180°
Turtle Object No 15

Formula
- \varphi_{i+1} = \varphi_i + 84° \cdot i^2-180°
Turtle Object No 16

Formula
- \varphi_{i+1} = \varphi_i + 132° \cdot i^2-180°
Turtle Object No 17

Formula
- \varphi_{i+1} = \varphi_i + 168° \cdot i^2-180°
Turtle Object No 18

Formula
- \varphi_{i+1} = \varphi_i + 78.75° \cdot i^2-180°
Turtle Object No 19

Formula
- \varphi_{i+1} = \varphi_i + 10° \cdot i^2-180°
Turtle Object No 20

Formula
- \varphi_{i+1} = \varphi_i + 50° \cdot i^2-180°
Turtle Object No 21

Turtle Object No 22

Turtle Object No 23

Turtle Object No 24

Turtle Object No 25

Turtle Object No 26

Turtle Object No 27

Turtle Object No 28

Turtle Object No 29

Turtle Object No 30

Turtle Object No 31

Turtle Object No 32

Turtle Object No 33

Turtle Object No 34

Turtle Object No 35

Turtle Object No 36

Turtle Object No 37

Turtle Object No 38

Turtle Object No 39

Turtle Object No 40

Turtle Object No 41

Turtle Object No 42

Turtle Object No 43