Richard Palais ve Luc Benard
Matematikçiler, öğretirken veya araştırırken kullandıkları matematiksel kavramların görselleştirilmesi için grafik sanatlardaki ileri teknikleri kullanagelmişlerdir. Şekilleri kuma çizmeden taş tabletlere kazımaya geçiş gibi… Bu yüzden bilgisayarların modern teknolojisini değiştiren köklü yeniliklerin, karmakarışık görünen matematiksel işlem ve nesneleri görselleştirmek için olağanüstü imkanlar sağlaması şaşırtıcı değil. Bu galerinin yaratıcıları, bu karışık nesneleri, yeni teknolojileri böyle kullanmak için tasarlanmış matematiksel görselleştirme programı 3D-XplorMath başta olmak üzere birkaç gereç yardımıyla inceliyor. 3D-XplorMath, matematikçi olmayanlara bile matematiğin farklı alanlarındaki görsel güzelliği deneyimlemeleri yolunu açacak yeni grafik imkanları sunan, sezgisel bir kullanıcı arayüzüne sahip sanal bir matematik müzesi olarak düşünülebilir.
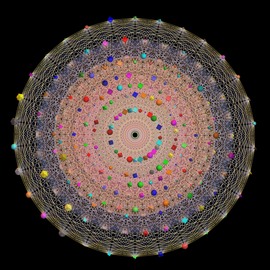
Lyapunov Oyunu
Markus-Lyapunov resimleri, Lyapunov üstelinin yatay, doğurganlığın dikey eksenlerde temsil edildiği renklendirilmiş resimlerdir. Resimlerde sadece kararlı alan çizilir; kaos (yani pozitif Lyapunov üsteli) koyu renklendirilmiştir. Üstel sıfırdan negatif sonsuza doğru giderken, rengin tonu açıktan koyuya değişmektedir. Sıfırda, yani kaosun eşiğinde, renk birdenbire koyudan açık bir tona dönüşür. Elbette bu renk tasarımında keyfi birçok seçim var. Bu da estetik yorumlar ve tercihler için fırsat oluşturuyor. Buradaki resim, üst üste bindirilmiş yedi tane orijinal Markus-Lyapunov resminden oluşmaktadır.
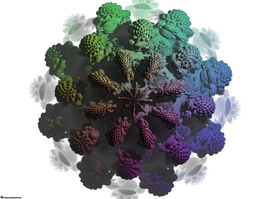
Equations Studies
These fractal images were produced by using various equations as input in Stephen Ferguson’s Flarium24 Windows program, us- ing 40 Iterations and the filter:
rr+=atan(fabs(dzy/dzx))*atan(fabs(dzx/dzy))*2
They were then assembled in PhotoShop using fonts and coloration to mimic the old technical drawings of Leonardo DaVinci. While these images are highly mathematical in origin, many people find them aesthetically appealing completely independent of their source.
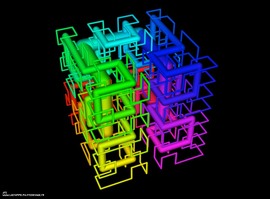
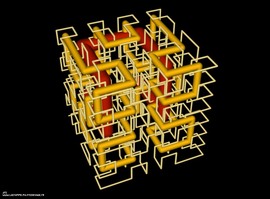
Üç yönde periyodik bir yüzey
4 (cos x cos y + cos y cos z + cos z cos x) – 3 cos x cos y cos z = -2,4
trigonometrik denklemiyle elde edilmiştir. Öncelikle örnek bir hücre oluşturalım: bir küpün ortasında bir odacık ve bu odacıktan küpün köşelerine ve yüzlerine birer boru döşeyin. Sonra bu hücrenin birbirine dik üç adet ötelemeyle kaydırarak kopyalarını alalım. Oluşan yüzeyin üç öteleme simetrisi olur. Bu yüzey, Alman matematikçi Karl Hermann Amandus Schwartz tarafından 1880’de (o zamanlar Halle, Göttingen ve Berlin’de profesördü) keşfedilen Schwartz minimal yüzeyine oldukça yaklaşıktır. Son zamanlarda, malzeme bilimciler bu minimal yüzeyi ve benzerlerini blok kopolimer olarak adlandırılan modellemeleri yapmak için incelemiştir.
Modelin aslı, David A. Hoffman’dan alınmıştır. Özgün model, güzel bir sahneye yerleştirilmiş ve Bryce’da ışıklandırılıp renklendirilmiştir.
Wada Havzaları
Gördüğünüz resim, kaotik dağılma deneylerinin çıktılarını yeniden üretiyor. Buradaki basit yapı, çok iyi yansıtan yüzeylere sahip dört adet birbirine eş topun, her biri bir diğerine dokunacak biçimde bir piramit halinde dizilmesiyle oluşuyor. Eğer öndeki üç topun arasındaki boşluğu incelerseniz, yansıyan görüntülerin üç boyutlu bir fraktal oluşturduğunu görürsünüz. Bu fraktal yapı, 1917 yılında buna benzer uzaysal bölümlenmeler üzerinde çalışmış Japon matematikçi T. Wada’nın adıyla anılan Wada Özelliğine sahiptir. Wada Özelliği, üç adet çekim havzası olan ayrık dinamik sistemlerle ilişkilidir. Bu havzalar öyle birbirinin içine geçmiştir ki bir havzanın topolojik kenarındaki her nokta aynı zamanda diğer bütün havzaların da kenarındadır. Bu görüntü Bryce programında bir araya getirilmiş, ışıklandırılmış ve renklendirilmiştir.
Beş Adet Cam Yüzey
Bu görüntü matematikçi Richard Palais ve grafik sanatçısı Luc Benard işbirliğinin sonucudur. Bu resim Ulusal Bilim Vakfı / Bilim Dergisi 2006 Görselleştirme Yarışmasının illüstrasyon kategorisinde birincilik ödülü almıştır. Science dergisinin 22 Eylül 2006 tarihli sayısına kapak resmi olmuştur.
Tasvir edilen beş matematiksel yüzey (sol alttan başlayarak ve saat yönünde): Klein Şişesi, Simetrik 4-Noid, Havalandırma Yüzeyi, Boy Yüzeyi ve Sievert-Enneper Yüzeyi.
Görüntüdeki yüzeyler Palais tarafından geliştirilen 3D-XplorMath programı kullanılarak oluşturulmuştur; bir araya getirme ve ışıklandırma-renklendirme Benard tarafından Bryce programıyla yapılmıştır.