Richard Palais y Luc Benard
Los matemáticos se han valido desde siempre de los avances en las artes gráficas para mejorar la forma en que muestran los conceptos matemáticos, tanto para enseñar como para investigar. Y dadas las nuevas posibilidades que brindan las computadoras modernas, no debería sorprendernos que las empleen también para generar visualizaciones de objetos y procesos matemáticos. Los autores de esta galería exploran esos objetos, usando entre otros, el software 3D-XplorMath, un programa diseñador para aprovechar estas nuevas capacidades. Este provee un virtual museo matemático con una interface de usuario intuitiva, que permite inclusive a personas ajenas a la matemática explorar la belleza inherente en las distintas áreas de la matemática.
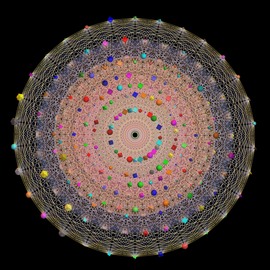
Representación Lyapunov
Mario Markus del Instituto Max Planck para la Nutrición (Max Planck Institute for Nutrition) ha usado sistemas dinámicos para estudiar la evolución de las poblaciones animales - el cambio a lo largo del tiempo respecto a la comida, fertilidad, tamaño, etc. - con la dinámica que requiere que la capacidad de reproducción alterne casi-periódicamente entre dos valores. Dichos sistemas pueden mostrar un ciclo estable y una evolución caótica dependiendo de la capacidad de fertilidad. La estabilidad o el caos pueden ser analizados al calcular el llamado exponente característico Lyapunov. (Lyapunov era un matemático ruso que vivió a finales del siglo XIX)
Las imágenes Markus-Lyapunov son mapeos de color del exponente característico Lyapunov en comparación con la fertilidad, en los ejes horizontales y verticales. Sólo se plotea el dominio de la estabilidad; aquí, el caos (es decir, el exponente positivo Lyapunov) se presenta en azul oscuro. Conforme el exponente va de 0 a menos infinito, los tonos van de lo claro a lo oscuro. En cero, el umbral del caos, el color súbitamente salta del azul oscuro a un tono más claro. Es obvio que hay mucho de arbitrario en este mapeo de color, y esto brinda una oportunidad para elecciones basadas en consideraciones estéticas. La imagen consiste en siete imágenes originales Markus Lyapunov que fueron reconstruidas y superimpuestas.
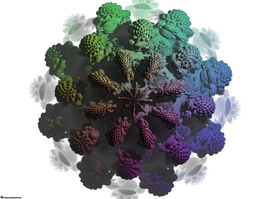
Estudios de Ecuaciones
Estas imágenes fractales fueron producidas usando diferentes ecuaciones como información de entrada en el programa de Windows Flarium24 de Stephen Ferguson, usando 40 iteraciones y el filtro:
rr+=atan(fabs(dzy/dzx))*atan(fabs(dzx/dzy))*2
Después fueron ensambladas en PhotoShop usando fuentes y coloración para imitar los viejos dibujos técnicos de Leonardo DaVinci. Mientras estas imágenes son altamente matemáticas en su origen, mucha gente las considera estéticamente atractivas de forma totalmente independiente de su origen.
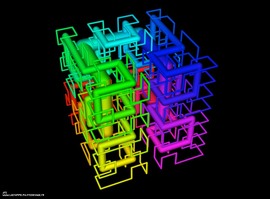
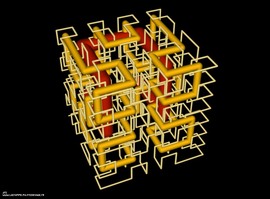
A Triply-Periodic Level Surface
Una superficie de nivel periódica triple
La superficie de color verde mostrada aquí tiene tres simetrías ortogonales translacionales. Es la superficie de nivel dada por la ecuación trigonométrica:
4*(cos x*cos y+cos y*cos z+cos z*cos x) - 3*cos x *cos y *cos z = -2.4
Una celda de unidad puede ser vista como una cámara central con tubos hacia las esquinas y caras del cubo. Esta superficie se aproxima cercanamente a la superficie-P mínima descubierta en 1880 por Karl Hermann Amandus Schwartz (quien fue Profesor en Halle, Gotinga, y Berlín). Recientemente ha sido investigada por científicos de materiales, quienes la usan y superficies relacionadas para modelar los llamados co-polímeros de bloque. El modelo original fue tomado de David A. Hoffman. Esto fue texturizado, colocado en una escena que sentimos que le aporta a la belleza del objeto y el renderizado se realizó con el software Bryce.
Autores Luc Benard
Licencia CC BY-NC-SA
Cuencas de Wada
… o las esferas del Guggenheim
Esta bella imagen, creada por Richard Palais y Luc Benard, es una reproducción en el ordenador de los resultados de ciertos experimentos de “dispersión caótica”. Ésta consiste en la iteración de una partícula con un sistema que se dispersa y su estudio tiene aplicaciones en dinámica de fluidos, cosmología, termodinámica, mecánica celeste y física de partículas.
La configuración básica está compuesta por cuatro bolas idénticas y muy reflectantes colocadas formando un tetraedro y de tal forma que cada bola toque a las otras tres, es decir, a la manera en que el frutero coloca las naranjas. Si se mira en el hueco entre tres bolas, las imágenes reflejadas que se ven forman un fractal tridimensional. Este experimento puede realizarse en casa con cuatro bolas de navidad reflectantes.
La obra “El gran árbol y el ojo” (2009) del escultor Anish Kapoor, que se encuentra en el exterior del Museo Guggenheim de Bilbao, es una versión libre, y con múltiples esferas espejadas que se reflejan unas en otras, del efecto de las cuencas de Wada.
Naturaleza muerta
Cinco superficies de vidrio sobre una mesa
Siguiendo la tradición de las “naturalezas muertas” (bodegones) de la historia del arte, el matemático Richard Palais y el artista gráfico Luc Benard han creado esta obra en la que los objetos son superficies matemáticas.
Las superficies de este bodegón tienen propiedades geométricas destacables e interés histórico, pero han sido elegidas principalmente por su belleza. Son, desde abajo a la izquierda y en el sentido de las agujas del reloj: la Botella de Klein (superficie no orientable, de una sola cara), el 4-noide simétrico (superficie minimal), la superficie pseudoesférica de tipo pulsante (ejemplo de superficie con una geometría no euclídea, de tipo hiperbólico, K<0), la superficie de Boy (superficie no orientable) y la superficie de Siervert-Enneper (ejemplo de superficie con una geometría no euclídea, de tipo elíptico, K>0).
Esta composición fue galardonada con el primer premio del Concurso de Visualización en Ciencia e Ingeniería de la revista Science y la National Science Foundation de EEUU.