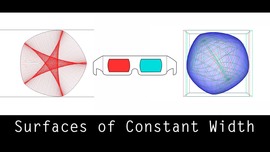
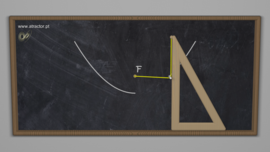
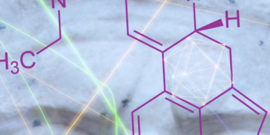
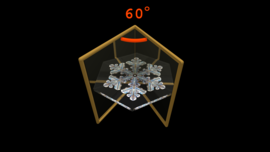
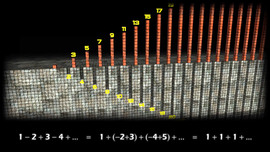
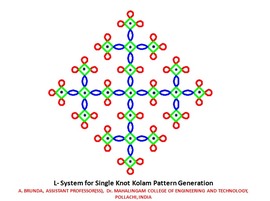
A “MathLapse” (ML) is a new educational and artistic format, which is supposed to highlight the link between mathematics and real-world phenomena. The name MathLapse is inspired by the timelapse-technique in physics: By re-scaling time, phenomena that we cannot observe with the naked eye are visualized.
A ML is short, simple, self-contained and creative and should illustrate a single mathematical idea through true or virtual animated images. The content of a ML is diverse. For example, it can be a geometric animation or a time-lapse video that comes with mathematical equations and/or concise explanations.