MathLapse - From Stereographic Projection to Mercator Map
film
Licence
Credits
There are two purposes in this animation
1. Use complex logarithm to see the relation between stereographic projection and Mercator map
2. By rotating small region to the poles we can make its image as large as we want without missing
other parts of the globe (except one point)
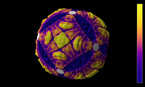
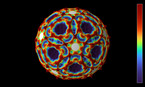
Stereographic Projection is a conformal (angle preserving) map from sphere (minus one point) to the infinite plane.
Complex log is a map from infinite plane (minous a branch cut) the infinite long strip.
The composition of these two gives the Mercator’s map.
This animation illustrates the transformation between image of stereographic projection and the image of Mercator’s map and demonstrates that we can enlarge small region in the Mercator’s map by rotating
the earth.
Files
More Films
