Site percolation on a lattice of triangles
film
Site percolation on a lattice of triangles
Licence
Credits
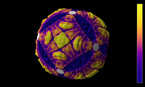
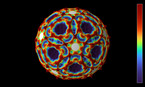
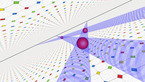
Bernoulli site percolation, on lattices of triangles of different sizes
The cells of the lattice are equilateral triangles. Their centers form a hexagonal lattice, whose Voronoi cells are the triangles.
The parameter p increasing from 0 to 1 is the probability that a triangle is open. Closed triangles are shown in purple, and open ones in yellow when they are connected to the left boundary, and pink otherwise. The increase of p slows down when it reaches the critical value, which is approximately equal to 0.69704. The graph shows the rsize of the percolation cluster (the set of open triangles connected to the left boundary), divided by the number of open triangles, as a function of p.