Waves with cubic symmetry on a sphere
film
Licence
Credits
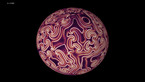
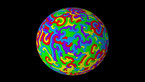
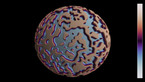
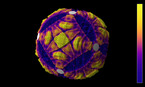
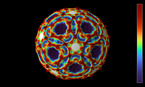
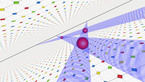
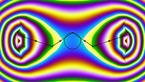
Solution of the wave equation on a sphere. Reflecting obstacles have been placed around the vertices of a cube. The initial state is composed circular waves concentrated at the centers of the faces of the cube, and on the midpoints of its edges. The colors and radial coordinate represent the wave height and averaged wave energy.
The simulation shows a solution of the wave equation on a sphere, obtained by a finite difference scheme. There are Dirichlet boundary conditions on a set of discs of constant radius placed on the vertices of a cube. The initial state is a set of circular waves concentrated near the centers of the faces of the cube, which form a regular octahedron, and on the midpoints of the cube’s edges.
Part 1 shows the wave height, and part 2 shows the energy flux.
Files
More Films
