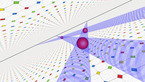
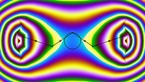
The film Epita-Dodecahedron will be screened in the program
Austrian Animated Experiments - 30 Years ASIFA AUSTRIA at the
Animated Dreams, 17th international Animation Film Festival, Tallinn (Estonia)
L'épitadodécaèdre pour visualiser l'espace dodécaédrique de Poincaré
films
Licence
Crédits
- Renate Quehenberger
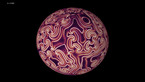
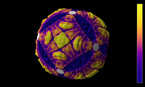
Tout comme le concept d’espace dodécaédrique par Henri Poincaré, l’épitadodécaèdre permet de visualiser le principe des contre-mouvements du polyèdre opposé E+ à la place des espaces pentagonaux, dans la description
de la sphère d’homologie de Poincaré que l’on trouve dans son «Cinquième complément». Cela montre clairement les différentes symétries apparaissant au fur et à mesure, se cristallisant après chaque rotation de 36°, conformément à la manière dont, en 1904, Poincaré imagina la forme de l’Univers.
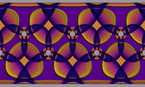
L’épitaèdre est un heptaèdre découvert récemment et fournit la représentation tridimensionnelle des cerf-volants et fléchettes des pavages de Penrose. Les longueurs des côtés ainsi que les volumes des épitaèdres – E- (concave), E+ (convexe) et l’assemblage des deux, EE (E- : E+ = E+ : EE ) – font apparaître le nombre d’or φ (≅ 1.618). Ainsi, les épitaèdres forment des pavages de l’espace gouvernés par le nombre d’or, à l’instar des Pavages de Penrose irréguliers du plan, qui est une tranche de l’espace de dimension 5.
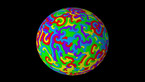
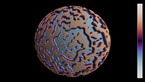
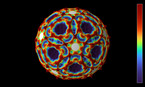
En assemblant 12 épitaèdres en un dodédaèdre appelé épita-dodécaèdre, un autre dodécaèdre apparaît naturellement au centre d’un espace de configuration complexe. Ceci est relié au fait qu’un épitaèdre peut être déplié à partir d’un unique pentagone, bien qu’il manque alors un triangle obtus (Quantum Cinema, 2012). Il peut donc être vu comme un pentagone tridimensionnel, ce qui montre que l’assemblage résulte nécessairement en des configuations de dimension plus grande. L’intersection des apex des 12 polyèdres forme 25 sous-espaces avec différentes formes au centre, en forme d’étoiles en raison des 60 faces. On y retrouve les 26 dimensions qui apparaissent en mécanique quantique. Au centre de l’épita-dodécaèdre, un autre petit dodécaèdre apparaît au sein d’une configurations complexe d’espaces s’intersectant. Jusqu’ici, nous avons pu identifier 4 formes solides centrales différentes : un dodécaèdre, l’icosaèdre, l’icosidodécaèdre appartenant au groupe des solides archimédiens et, jusqu’ici non-mentionné, l’icosidodécaèdre étoilé. Les cellules en pyramides pentagonales, qui s’appuient sur chaque face du dodécaèdre, forment le petit dodécaèdre étoilé.
L’espace dodécaédrique basé sur l’idée de Poincaré a été explicité par Threlfall et Seifert, qui ont caractérisé en utilisant un dodécaèdre les faces opposées identifiées après une rotation de pi/5. Il porte l’adjectif «sphérique» car il est borné par des pentagones sphériques, étant obtenu comme l’intersection de 12 boules (Threlfall et Seifert, 1931).
De la même manière que ce concept, l’épitadodécaèdre permet de visualiser le principe des contre-mouvements des polyèdres opposés E+, au lieu des espaces pentagonaux de la description par Poincaré de la sphère d’homologie dans son «Cinquième complément». Ainsi, on voit clairement les différentes symétries apparaissant au fur et à mesure, se cristallisant à chaque rotation de 36°, comme Henri Poincaré l’anticipa en 1904.
Ainsi, cette unique cellule de l’espace de dimension supérieure permet l’assemblage en un espace indéfiniment remplissable qui possède un bord ayant la forme d’un dodécaèdre, de manière similaire, le bord d’un motif de Penrose, un pentagone avec une forme décagonale ayant le même axe de symérie.
L’artiste-scientifique Arthur I. Miller résume :
Le cinquième élément - la quintessence - a une forme géométrique en épitaèdre tandis que nous vivons dans un espace de Poincaré dodécaédrique, nommé d’après le mathématicien français Henri Poincaré. (Miller, 2013)