LPDJLQH D VHFUHW
films
Crédits
- Idea
- Conception
- Realization and Production
- Surfer Movies
- Original Music
Voyage artistique dans le monde de la cryptographie sur les courbes elliptiques.
Les triplets pythagoriciens comme (3, 4, 5) ou (4961, 6480, 8161) étaient bien connus des Babyloniens autour de 1600 av. J-C. Ils connaissaient également leur correspondance avec les triangles rectangles à cotés entiers et le problème consistant à scinder un carré donné en deux carrés. Bien que de tels triplets aient été étudiés en détail depuis le temps d’Euclide, autour de 300 av. J-C, ce fut seulement au milieu du XVIIème siècle que Pierre de Fermat formula l’observation suivante : « il est impossible de partager soit un cube en deux cubes, soit un bicarré en deux bicarrés, soit en général une puissance quelconque supérieure au carré en deux puissances de même degré »
Ceci devint le fameux « dernier théorème de Fermat » établissant que l’équation a^n+b^n=c^n n’a pas de solution entière non nulle dès lors que n est plus grand que deux. Il a été prouvé entièrement en 1994, à peu près trois siècles et demi plus tard, utilisant la théorie des courbes elliptiques… développée au XXème siècle !
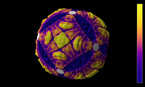
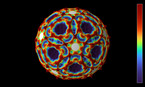
Les courbes elliptiques ont de belles et profondes propriétés. Ce sont des courbes planes du type y²=x³+a·x+b et qui ont été étudiées depuis le XIXème siècle. Cette équation dans le plan affine correspond à l’équation homogène y²z= x³ + a·xz² + b·z³ qui décrit dans l’espace une famille de surfaces algébriques à deux paramètres a et b. La variation computationnelle de ces équations génère de belles animations qui stimulent notre imagination et évoquent notre créativité mathématique.
La cryptographie est un ensemble de méthodes sûres permettant de transmettre et protéger informations précieuses et secrètes. Depuis 1977, le système de chiffrement asymétrique RSA est largement utilisé. Il est basé sur la théorie des nombres premiers et sur la difficulté de factoriser les grands nombres entiers. Suite à l’impact de la méthode des courbes elliptiques pour la factorisation d’entiers, les mathématiciens ont inventé en 1985 la cryptographie sur les courbes elliptiques (ECC, pour « Elliptic Curve Cryptography » en anglais) et, depuis, la sophistication mathématique de la cryptographie a été portée à un tout autre niveau.
La sécurité des algorithmes ECC est basée sur le problème logarithmique des courbes elliptiques qui semble être un des plus grands problèmes de l’arithmétique des corps finis. Les avancées récentes laissent entendre qu’un certain niveau de sécurité désiré peut être obtenu avec des clefs significativement plus petites, par exemple, qu’une clef ECC de 160 bits fournit le même niveau de sécurité qu’une clef RSA de 1024 bits.
La théorie des courbes elliptiques illustre la beauté des liens entre la théorie des nombres, l’algèbre et la géométrie et fournit un puissant outil mathématique pour renforcer la sécurité du commerce électronique et des communications. La vielle et peu fiable méthode de chiffrement par décalage, utilisant la trop simple opération mathématique consistant à chiffrer un message dans l’alphabet usuel au moyen de la formule d = c - 3 (mod 26) est obsolète. Cependant, elle nous donne la clef pour déchiffrer le titre de ce film :
_ _ _ _ _ _ _ _ _ _ _ _ _ _
Pour télécharger le film en haute résolution en portugais, allemand, anglais et espagnol, visitez : http://www. cim.pt/LPD-UHW