An exhibition that explores the link between contemporary art and mathematics, at the Centro Cultural Kirchner, Buenos Aires, Argentina.
MathLapse - Recipe for a Wild Knot
films
Licence
Crédits
- Animation
- Sound Design
- Pseudo-Random Generated Music
- Edition
- Graphic Design
- Text in the description
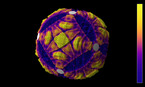
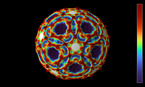
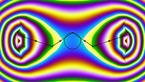
MathLapse Festival 2016 Winner. A Wild Knot is a circular curve in the three-dimensional space which is infinitely knotted. In this video we show a recipe to build some kind of Wild Knots, using reflections on several spheres which are strung on a necklace.
This recipe to construct a Wild Knot is the following:
Pick up a circular string of beads into the three dimensional space, keeping all the beads disjoint, except for the points of tangency. Cut it open in a point of tangency, tie a knot in the string, and close it up again, still keeping all the beads disjoint, except for the points of tangency. The knot keeps reproducing itself under the various reflections in the group infinitely many times. In the limit, this construction yields a wild knot.
In other words: If we string together a certain number of spheres into a knot we would have a true knotted necklace. If we also assume that all the spheres in the necklace are perfectly reflective, as if they were made of mirror, we could observe an image of the whole necklace in each one of the spheres, conforming a new necklace of smaller spheres. This new necklace is also knotted. In fact, it reproduces the original knot in each sphere, and so on. The repetition of this procedure infinitely many times yields a Wild Knot.