Hiltrud Heinrich
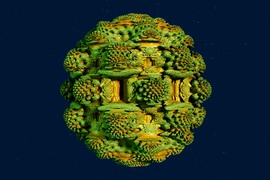
The German artist Hiltrud Heinrich used her pictures in own math art exhibitions. The pictures are of abstract and aesthetic nature. She also replicated the design of the SURFER pictures as patterns for patchwork quilts.

Formula
- (x^2+y^2-1-x^2y^2z^2)+(x^2+y^2+z^2-3)\cdot xy^4+yx^4=0
Entsprechung (counterparts)

Formula
- (y \cdot (ax^4+bxy^2+ayz* y^2)^2*(8x^2)*(z^3+ 6z^2)+(9z-25)*5x-zy^2=0 , \\ a=0.04 \quad b=1.00
Aufbruch (the burst)

Formula
- (x^2+y^2+z^2-5)\cdot(x+y)^4-(x^2y^2z^2-1)=0
crab

Formula
- (x^4y+x^3y^2)+(x^4y-10x^4y^3+y^3)^2-z^2\cdot((x^2+y^2+z^2-9)\cdot(b-x^3y^2z^3))=0
Bewegung (movement)

Formula
- ((x^2+y^2+z^2-9)^3-x^2y^2z^2)\cdot(x^2+y^2+z^2-0.5)\cdot xy^2+yx^2+xz=0
l´être originaire dans l´oeuf
Normal
0
21
false
false
false
MicrosoftInternetExplorer4
/* Style Definitions */
table.MsoNormalTable
{mso-style-name:”Normale Tabelle”;
mso-tstyle-rowband-size:0;
mso-tstyle-colband-size:0;
mso-style-noshow:yes;
mso-style-parent:”“;
mso-padding-alt:0cm 5.4pt 0cm 5.4pt;
mso-para-margin:0cm;
mso-para-margin-bottom:.0001pt;
mso-pagination:widow-orphan;
font-size:10.0pt;
font-family:”Times New Roman”;
mso-ansi-language:#0400;
mso-fareast-language:#0400;
mso-bidi-language:#0400;}
table.MsoTableGrid
{mso-style-name:Tabellengitternetz;
mso-tstyle-rowband-size:0;
mso-tstyle-colband-size:0;
border:solid windowtext 1.0pt;
mso-border-alt:solid windowtext .5pt;
mso-padding-alt:0cm 5.4pt 0cm 5.4pt;
mso-border-insideh:.5pt solid windowtext;
mso-border-insidev:.5pt solid windowtext;
mso-para-margin:0cm;
mso-para-margin-bottom:.0001pt;
mso-pagination:widow-orphan;
font-size:10.0pt;
font-family:”Times New Roman”;
mso-ansi-language:#0400;
mso-fareast-language:#0400;
mso-bidi-language:#0400;}

Formula
- ((x^2+y^2+z^2-10)^6+x^2y^2z^2)+(x^5+y+z+0.5)^2\cdot xy^3+yx^6+yz=0
Farbe und Linien (colour and lines)

Formula
- 6x^2-2x^4-y^7z^2+x^2y^2z^2\cdot(x^2+y^2+z^3)-4=0
genmanipulierter Pfau

Formula
- (x^2+y^2+z^2-3)\cdot xz^2+(x+z)^4=0
ohne Namen 2 (without a name)
Normal
0
21
false
false
false
MicrosoftInternetExplorer4
/* Style Definitions */
table.MsoNormalTable
{mso-style-name:”Normale Tabelle”;
mso-tstyle-rowband-size:0;
mso-tstyle-colband-size:0;
mso-style-noshow:yes;
mso-style-parent:”“;
mso-padding-alt:0cm 5.4pt 0cm 5.4pt;
mso-para-margin:0cm;
mso-para-margin-bottom:.0001pt;
mso-pagination:widow-orphan;
font-size:10.0pt;
font-family:”Times New Roman”;
mso-ansi-language:#0400;
mso-fareast-language:#0400;
mso-bidi-language:#0400;}
table.MsoTableGrid
{mso-style-name:Tabellengitternetz;
mso-tstyle-rowband-size:0;
mso-tstyle-colband-size:0;
border:solid windowtext 1.0pt;
mso-border-alt:solid windowtext .5pt;
mso-padding-alt:0cm 5.4pt 0cm 5.4pt;
mso-border-insideh:.5pt solid windowtext;
mso-border-insidev:.5pt solid windowtext;
mso-para-margin:0cm;
mso-para-margin-bottom:.0001pt;
mso-pagination:widow-orphan;
font-size:10.0pt;
font-family:”Times New Roman”;
mso-ansi-language:#0400;
mso-fareast-language:#0400;
mso-bidi-language:#0400;}

Formula
- ((x^2+y^2+z^2-7.5)^3+x^2+z^2-x^2y^2z^2)+ab\cdot(x^2+y^2+z^2-0.5)\cdot xy^3+yx^4+yz=0 \\ a=0.02 \quad b=0.02
Fratze (grotesque face)

Formula
- (x^4y+x^3y^2)+(x^4y-10x^4y^3+y^3)^2-z^2\cdot((x^2+y^2+z^2-9)\cdot(b-x^3y^2z^3))=0
Karneval in Venedig 2 (Venetian carnival )

Formula
- (x^2+y^2+z^2-5)\cdot xyz+(x+y)^3-(x^2y^2z^2-1)+2x4y=0
Faszinierende Unterwasserwelt 1 (fascinating marine world)
Normal
0
21
false
false
false
MicrosoftInternetExplorer4

Formula
- ((x^2+y^2-1)^3-x^2y^2z^2)\cdot(x^2+y^2+z^2-3)\cdot xy^3+yx^3+xz=0
Zartes Etwas 2 ( delicate something)

Formula
- ((x^2+y^2+z^2-9)^3-x^2y^2z^2)\cdot(x^2+y^2+z^2-3)\cdot xy^3+yx^3+xz=0
Flugkörper (projectile)

Formula
- (x^2-z^3+x^3-y^2+(y^4z)^3+x^2+z^3)\cdot((x^2+y^2+z^2)^2-9\cdot(x^2+y^2))=0
Kongresshalle (convention hall)
Normal
0
21
false
false
false
MicrosoftInternetExplorer4

Formula
- 6x^2-2x^4-y^7z^2+x^2y^2z^2+(x^2+y^2+z^5)-1=0
Muster a ( pattern)

Formula
- 20x^2-2x^6-y^5z^2+x^2y^2z^2\cdot(x^2+y^2+z^5)-11=0