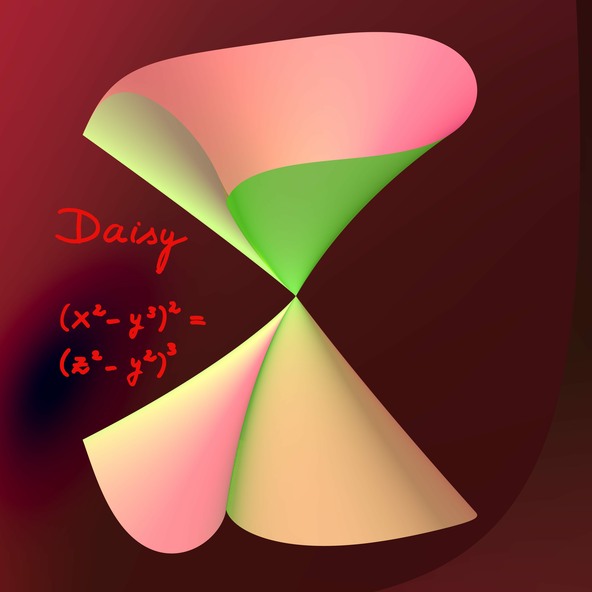Maths can be beautiful! On June 6th at 11 am, two new interactive stations will be presented at the EXPERIMINTA ScienceCenter in Frankfurt, Germany. At the opening Prof. Oldenburg, Goethe-Universität in Frankfurt, and Dr. Matt, Mathematisches Forschungsinstitut, Oberwolfach will be present. The two stations are accompanied by a gallery of beautiful visualizations and will be permanently displayed at the science center.
Herwig Hauser Classic
Herwig Hauser의 고전적인 대수곡면들은 원조 Imaginary 전시회를 위해 수집되어있습니다. Hauser의 형식과 공식들은 방정식들이 단순하고 아름답도록 선택되었습니다. 이 그림들은 평범하고 자연스럽고 흥미로운 기하학적 사실들을 보여줍니다. Hauser는 University of Vienna의 교수이며 대수기하와 특이점 이론을 연구합니다.
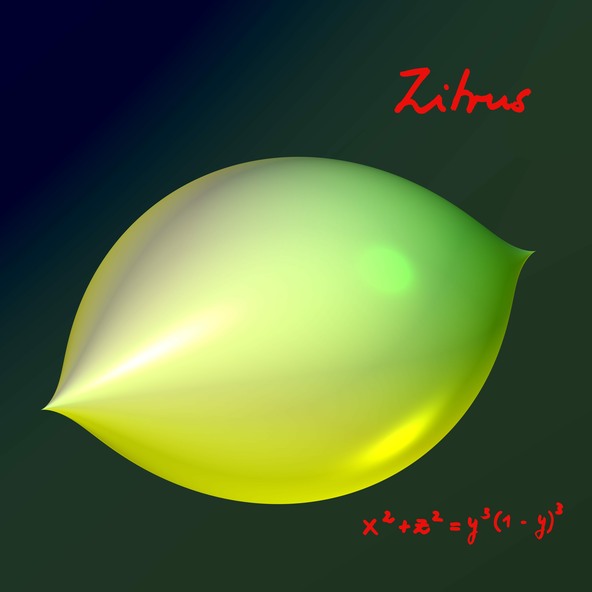
Zitrus (Citric)
레몬의 방정식 x2+z2 = y3(1−y)3 은 그림만큼 간단합니다. 곡면의 2개의 뾰족점은 회전축의 양 끝에 존재합니다.
(1−y)3 항을 없애고 얻은 x2+z2 = y3 은 한 개의 뾰족점만 갖고, x2+z2 = (1−y)3 은 거울상(대칭 이미지)을 만들어 줍니다. 두 곡면 모두 무한곡면이지만 두 식을 결합하여 유한곡면 레몬을 얻습니다. 만약 y가 1보다 크면 우변은 음수가 되고 좌변은 항상 양수이기 때문에 이를 만족하는 x와 z가 존재하지 않게 됩니다.
Limão
방정식 x2 = y3z3으로 표현되는 대수 곡면은 시각화가 쉽지 않습니다. 곡면 그 자체를 최대한 표현하는데 있어 음영과 원점 주변의 기이한 모양 표현이 걸림돌이 됩니다. 이는 기하학적 모양 그리고 무엇보다도 어떤 방향에서 바라보는지에 따라 크게 다릅니다.
그래서 수학적 사실과는 다르게 인공적으로 얼룩을 넣어 표현하였습니다. 반사효과 역시 곡면을 이해하는데 있어 방해 요소가 될 수 있습니다. 이 그림에서는 모서리를 따라서 교점에 가까워질수록 색이 옅어지는 것을 볼 수 있습니다.
특이점 주변에서 식을 풀기가 어렵기 때문에 이러한 문제점이 발생합니다. 해결책 중 하나는 곡면의 매개변수화 있는데 이는 많은 경우에 효과적으로 이용됩니다.
Vis á Vis
Vis a Vis 는 ‘서로 반대다’ 라는 것을 의미하며 이 그림에서는 두 개의 대수기하학적 현상이 대조되는 형태를 보여줍니다.
좌측곡면에는 뾰족점이 나타나 있지만 우측 곡선은 매끄럽게 표현되어 있습니다. 방정식이 다양하게 변할 때, 매끄러운 점에서 발생하지 않는 예측 불가능한 현상이 특이점에서는 발생하기 때문에 더 흥미롭습니다.
이 곡면은 직관을 통해 매우 쉽게 만들어낼 수 있습니다. 방정식과 그에 해당하는 곡면을 비교하하는 것은 흥미롭게 대수곡면을 이해하는 방법입니다.
Calypso
x2+y2z = z2으로 표현되는 대수곡면 Calypso는 세 개의 직선을 포함합니다. 수평 직선은 명확하게 볼 수 있으며 이것은 상부와 하부가 만나는 원점을 통과합니다. 다른 두 개의 직선은 수직 평면에 놓여있습니다. 이 두 직선 또한 원점을 지납니다. 위의 두 직선으로 이루어진 평면으로 표면을 자른 단면은 두 개의 직선을 포함합니다.
이 평면을 조금 앞으로 이동시키면 단면의 곡선은 쌍곡선으로 바뀝니다. 이것은 계산을 통해 쉽게 확인할 수 있습니다. 먼저 y=0 또는 y=1이라고 놓으십시오. y=0인 경우 x2 = z2또는 (x−z) (x + z) = 0를 얻으며 이는 평면상의 두 직선의 식입니다. y=1인 경우 x2+z=z2 을 얻습니다. 이것은 x2+(z−1/2)2 = 1/4로 다시 적을 수 있으며 (0,1/2)를 중심으로 갖는 쌍곡선의 방정식입니다.
Calyx
x2+y2z3 = z4을 갖는 대수곡면 Calyx 는 특이점들의 집합인 직선을 포함하고 있습니다.
곡면의 아랫부분은 직선을 따라 뾰족한 특이점들을 갖는 반면, 윗부분을 그 직선을 접선으로 하
여 다른 부분과 원점에서 만납니다. 옆의 그림에서는 주어진 방정식이 기약 다항식이고 그에 해당하는 하나의 대수적 성분을 가진다는 점에서 오해의 소지가 있습니다.
Calyx가 Calypso사영 이미지라는 것을 보일 수 있습니다. 삼차원 공간에서 원기둥은 Calyx의 직선으로 퇴화됩니다. 대수적으로 그 사상은 Calyx 방정식 x2+y2z3 = z4에서 x를 xz 바꾸고 양변에서 인수 z2을 없애면서 정의할 수 있습니다.
Daisy
데이지 방정식 (x2−y3)2 = (z2−y2)3 을 미분하면 알 수 있듯이, 이 식의 특이점들은 교차하는 두 자취로 구성되어 있습니다. 특이점들을 더 잘 이해하기 위해 기하학자들은 그 것을 폭발(blowups)이라는 개념으로 특이점의 해소법(resolution)을 구성합니다. 유한번의 폭발로 원래 다양체를 그림자로 갖으면서 특이점이 없는 다양체를 만들 수 있습니다.
Diabolo
Diabolo 방정식 x2 = (y2+z2)2 은 (x−y2−z2)(x+y2+z2) = 0 으로 인수분해 될 수 있습니다. 그러므로 이에 해당하는 대수곡면은 두 개의 포물선을 회전시킨 곡면 x = ±(y2+z2) 을 합친 형태입니다. 이 두 곡면은 원점에서 접합니다. 이 접점은 위의 인수분해 식에서일차항 를 통해 대수적으로 이해할 수 있습니다. 이 때 접평면은 x=0이 나타내는 수직평면입니다.
그림의 줄무늬들은 조명에 의한 그림자 때문에 생깁니다. 만약 x2 = (y2+z2)2+1/1000처럼 원래방정식에 상수를 더해서 Diabolo 방정식을 변형시키면 두 곡면은 완전히 분리됩니다. 그리고 식에서 x 를 x+y 로 치환하면 두 곡면이 살짝 어긋나게 되는데요, SURFER를 이용해 확인해보세요!
Ding Dong
x²+y²+z³ = z² 으로 표현되는 곡면 Ding Dong은 IMAGINARY에서 가장 먼저 표현하려고 했던 대수곡면입니다. 모양은 쉽게 묘사할 수 있습니다. 그리스어 알파를 z축을 중심으로 회전시키면 얻을 수 있습니다. 그러나 컴퓨터를 이용하여 초록색의 표면을 표현하려고 할 때 문제가 발생하였습니다. 표면의 삼차원 시각화에서 녹색은 일반적으로 더 까다롭습니다. 그 뿐만 아니라 무광 또는 노랗게 표현되는 경향이 있었습니다.
빛과 반사 효과가 잘 나타나야 합니다. 공간 효과를 강화하는 옅은 파랑의 짙은 그림자를 확인해 보십시오.
Distel (Thistle)
x2+y2+z2+c(x2+y2)(x2+z2)(y2+z2) = 1으로 표현되는 대수곡면 엉겅퀴는 매우 특이한 대칭성을 갖습니다. 사실 위의 그림은 매우 큰 c 값으로 만들어진 대수곡면입니다. 여섯 개의 스파이크 모두 세 개의 유클리드 좌표축 위에 있습니다. 세 좌표축을 재배열 하더라도 엉겅퀴는 본래의 모양을 유지합니다. 결과적으로 이 입체의 대칭군은 정육면체 그리고 그 쌍대(dual)인 정팔면체의 대칭군과 같은 구조를 갖습니다.
별 모양의 대수곡면이 가질 수 있는 스파이크의 개수에는 놀랍게도 군 이론이라는 수학적 개념이 숨겨져 있습니다. 이론에 따르면 대수곡면은 4, 6, 8, 12 혹은 20개의 스파이크만 가질 수 있습니다. 여러분이 그 방정식을 찾아보세요!
Dullo
타원형의 경기장에 있는 축구팬들이 자신들이 응원하는 팀이 골을 넣었을 때 내는 환호성은 빠르게 팽창하는 고무링 모양으로 퍼져나갑니다.
눈 깜짝할 사이에 이 고무링 모양의 음파는 경기의 킥오프를 했던 중심에 도달하게 됩니다. 사방에서 발생한 음파가 중심에서 동시에 만나고 증폭됩니다.
이는 심판들이 왜 경기 중에는 항상 공 근처에 있도록 훈련 받는 이유입니다. 그래서 심판들은 골이 터졌을 때 절대 경기장의 중앙에 있지 않습니다. 진짜 골이 들어갔는지 확인하는 것도 있지만 고막이 찢어질지도 모르니까요!
Eistüte (Cone)
이 모양의 횡단면은 장미 모양의 리본과 같은 곡선입니다. 큰 원의 안쪽에 톱니바퀴를 따라 바깥쪽에 톱니바퀴가 있는 작은 원에 연필을 꽂아 돌리는 스파이로그래프(Spirograph)라는 도구를 이용해 이 곡선을 만들 수 있습니다.
스파이로그래프를 이용해 곡선을 만들 때 그 모양은 큰 원과 작은 원의 반지름의 비율에 의해 결정됩니다. 이 비율이 유리수일 때 닫힌 곡선을 얻을 수 있습니다.
위 모양의 아이스크림 콘을 만들면 무려 네 스쿱을 먹을 수 있겠네요.
Helix
Lemniscate 곡선은 방정식 y4+z2 = y2. 으로부터 표현되는 평면 곡선으로 원의 방정식 y2+z2 =1 에서 z를 z/y 로 치환하여서 얻을 수 있습니다. 이 치환은 기하학적으로 원을 숫자 8 모양의 루프로 변형시키는 것에 해당됩니다. y4+z2 = y2을 x,y,z 세 개의 변수의 식으로 이해하면 이 방정식의 해 집합은 삼차원 공간의 곡면입니다. 이 곡면은 바닥이 lemniscate인 기둥 모양입니다.
Helix 방정식은 y4+x2z2 = y2 은 위의 식에서 z를 zx로 치환하여 얻을 수 있습니다. 기하학적 관점에서 이 작업은 접는 것의 일종입니다. x와 z 사이의 대칭성은 식으로부터 쉽게 알 수 있습니다. 그 다음 우리는 계수 2 와 6을 넣는데 이는 원래의 helix를 살짝 늘려줍니다. 0이 아닌 c에 대해 Helix를 x=c 혹은 z=c 로 자르면 lemniscates를 얻고 y=c로 자르면 쌍곡선을 얻습니다.
Herz (Heart)
매우 간단한 방정식 y2+z3 = z4+x2z2을 가짐에도 불구하고 Heart 는 매우 미묘한 국소적(local) 그리고 대역적(global) 구조를 갖습니다. 특이점을 모은 집합은 직선을 이루며 그 직선은 이 곡면과 교차합니다. 그 직선과 수직인 평면 x=c 와 곡면 Heart의 교집합은 고리(loop)인데, c가 0에 접근함에 따라 매듭처럼 줄어 듭니다. 여기서 깔대기 모양이 만들어 집니다.
멀리서 바라보면 원형의 구멍을 볼 수 있습니다. 사실 xy 평면으로 자른 단면도 원입니다. 사실 이 곡면은 단순한 구조를 갖기 때문에 눈을 감고도 머릿속에 비교적 정확하게 그려낼 수 있습니다. 하지만 이를 말로 설명하는 것은 상당히 어려운데 이는 언어적 한계 때문입니다.
Himmel & Hölle (Heaven and Hell)
동서남북이라는 종이 접기를 기억하나요? 손가락 양손의 엄지와 검지 네개를 접힌 종이 밑에 끼워 두 방향으로 펼침으로써 각각 네 개의 안쪽 면을 볼 수 있는 형태이죠.
이 그림은 동서남북이라는 종이접기를 생각나게 합니다. 여덟개의 면을 파랑색과 빨간색으로 칠한다음 우리의 운명을 예측할 수 있는 게임이죠. 그래서 이 곡면의 이름을 천당과 지옥이라고 지었습니다.
y와 z의 차수를 모두 더하여 차수 4를 얻습니다. 이것은 4차 방정식이라 불리워지며 높은 차수일수록 곡면을 계산하기 더 복잡합니다.
Kolibri (Hummingbird)
여러분은 아마 Hummingbird 가 Heart 라는 대수곡면을 원점주변에서 확대하여 뒤집어 놓은 모양임을 눈치채셨을 겁니다. Hummingbird 방정식은 x3+x2z2 = y2이고 Heart 방정식은 y2+z3 = z4+x2z2으로써 매우 유사한 형태를 가집니다. 사실 아주 좋은 좌표변환을 통해 한 식에서 다른 식을 유도할 수 있습니다.
사실 벌새는 가장 작은 새 중에 하나로 매우 놀라운 능력을 가지고 있습니다. 일초에 200회 이상 날개를 펄럭일 수 있고 이 힘으로 날아다닐 수 있습니다. 이러한 활동은 많은 에너지를 필요로 하며 벌새가 매일 자신의 몸무게 두 배 이상의 음식을 먹는 이유입니다. 지속적인 음식 보충이 없으면 단 몇 시간 내에 벌새는 배고픔을 느낍니다. 또한 밤에는 체온을 낮춤으로써 에너지를 절약합니다.
Kreisel (Spinning Top)
위의 팽이 모양을 만드는 대수 방정식을 찾는 것은 굉장히 창의적인 수학적 아이디어를 필요로 합니다. 언뜻 보기에는 이 곡면을 표현하는 방정식이 어떤 형태를 가져야 할지 수학적으로 명확하지 않을 수도 있습니다.
이 곡면으로부터 우리는 방정식이 60(x2+y2)z4 = (60−x2−y2−z2)3 의 형태와 같아야 함을 유추할 수 있는데 그 이유는 다음과 같습니다. 먼저 팽이 모양이 z 축을 기준으로 한 회전체라는 사실로부터 다항식 x2+y2 이 포함되어야 함을 알 수 있습니다. 우변의 세제곱은 양 끝에 뾰족점을 만들기 위해 필요합니다. 그리고 z가 짝수 거듭제곱을 가져야 곡면이 xy평면에 대해 대칭인 형태를 갖습니다. 우변의 상수 60은 곡면의 미를 살리기 위해 선택된 숫자입니다.
Miau
이 곡면은 지루한 기차여행 중에 우연히 만들어졌습니다.(지루한 여행에서 대수 곡면 만들기 놀이를 하면 시간이 아주 빨리 간답니다!)
이 곡면을 만드는 방정식을 유도하는 것은 아주 어렵습니다. 왜냐하면 두 개의 구멍과 파묻혀 있는 특이점을 갖기 때문입니다.
수학자들에게 있어 방정식과 그에 해당하는 곡면을 탐구하는 것은 보물찾기와도 같습니다.
Nepali
다음의 Nepali 방정식 (xy−z3−1)2 = (1−x2−y2)3을 관찰하여 봅시다. 여기서 이차항 x2+y2과 xy 가 곡면의 회전대칭구조를 설명해 줍니다. z=c 에 의한 단면은 거의 원과 같은 곡선입니다. 방정식이 제곱과 세제곱 항을 모두 포함하고 있기 때문에 곡면이 위로 갈수록 얇아지는 구조를 갖게 됩니다..
경계부분의 곡선은 정확한 원이 아닌 모자의 챙처럼 구부러진 형태입니다. 하지만 이를 xy 평면에 사영시키면, 즉 위에서 바라보면 원입니다. 또한 이 곡면은 유한 곡면인데 이 사실은 방정식을 분석해보면 도출해낼 수 있습니다.
Seepferdchen (Seahorse)
이 곡면의 방정식을 찾는 것은 결코 쉬운 일이 아닙니다. 매끄러운 접점은 식에 약간의 변화만 주어도 사라지기 때문입니다.
이 대수곡면의 흥미로운 특성 중 하나는 이 곡면을 뒤 혹은 옆에서 바라보면 아주 조잡스럽게 보인다는 점입니다.
해마의 라틴어 이름은 Hippocampus이고 해마들은 열대와 온대기후 지역 전세계에 서식하고 있습니다.
Solitude
Solitude의 방정식 x2yz+xy2+y3+y3z = x2z2으로만은 이 곡면이 가지는 놀라운 기하학적 성질을 알 수 없습니다. 심지어는 옆의 그림도 여러 특징 중 일부만 보여줍니다.
그림에서 쉽게 확인할 수 있다시피 두 개의 큰 구멍과 작은 구멍이 있습니다.
위에서 바라보면 면에 수직한 한 직선을 볼 수 있는데 이에 수직한 단면은 매우 뾰족한 곡선입니다. 이 Solitude 라는 대수곡면은 눈에 보이는 기하학 형상을식으로부터 추론하는 것이 얼마나 어려운가를 보여줍니다. 비슷하게 우리는 정수론적 기하나 복소기하에 대해 질문을 던질 수 있습니다.
Tanz (Dance)
Dance 곡면을 기술하는 방정식 2x4 = x2 +y2z2에서 z=0 으로 놓으면 Dance 곡면과 xy-평면의 교선을 기술하는 방정식 2x4 = x2을 얻습니다. 이 식을 인수분해 하면 x2(√2x+1) (√2x−1) = 0 을 얻는데 이는 세 개의 평행선을 나타냅니다. 여기서 우리는 직선 x=z=0 이 Dance 곡면에 속하고 일차원의 고립된 구성요소임을 알 수 있습니다. 왜냐하면 x=0 주변에서 Dance 방정식의해가 x=y=0 혹은 x=z=0 즉, y축 z축 밖에 없기 때문입니다.
직선은 무한히 얇기 때문에 SURFER 같은 시각화 프로그램에서는 표현이 되지 않습니다. 그러므로 해 집합 중 직선 같은 1차원 요소들은 아주 얇은 원통으로 바꿔 따로 표현해야 합니다.
Taube (Dove)
Dove 곡면은 방정식 256z3 − 128x2z2+16x4z+144xy2z−4x3y2−27y4 = 0 에 의해 정의됩니다.
거듭제곱형태의 계수들은 결코 우연하게 만들어진 것은 아닙니다. 이는 판별식 이라는 더 일반적인 공식에서 파생된 것입니다. 이 식은 어떤 4차식의 판별식으로써 곡면의 음영 및 형태를 잘 기술합니다.
윤곽선의 형태는 곡면과 그 곡면의 사영 이미지 혹은 식으로부터 명확하게 알 수 있습니다.
Tülle (Nozzle)
Nozzle 이라는 대수곡면은 세 개의 매끈한 곡면으로 이루어져 있으며 이들의 교선 역시 매끄러운 평면 곡선입니다. 즉 세 개의 매끄러운 곡선을 얻을 수 있는데 이 중 둘은 포물선이고 나머지 하나는 직선입니다. 주목할만한 점은 포물선이 직선에 접한다는 것입니다. 이 그림에서는 세 개의 곡면이 서로 가로지르지만 그들의 교선은 서로 가로지르지 않습니다.
두 매끈한 곡면이 서로 가로지를 때 생기는 교선은 매우 중요한 기하학적 개념을 가지고 있습니다. 아이디얼 이론에 의하면 이 교선은 정확한 대수적 방법에 의해 구해질 수 있으며 계산과 증명에 이용될 수 있습니다. 하지만 특이점을 가지는 곡면에 대해서는 ‘가로지른다’ 라는 것이 여전히 정의되지 않습니다.
Zeck (Tick)
간단한 방정식 x2+y2 = z3(1−z) 은 Tick이라 불리는 곡면의 기하학적 성질을 완벽하게 반영합니다. 특이점과 모양, 곡률 등은 다음의 네 단항식 x2, y2, z3, z 에 의해 정의됩니다. 이를 통해 우리는 방정식이 복잡한 대수 곡면을 간단히 암호화하는 아주 효율적인 방법이라는 것을 알 수 있습니다.
하지만 명심해야 할 점은 곡면의 기하학적 성질이 식으로부터 항상 쉽게 도출되지는 않는다는 것입니다.. 다시 말하면, 주어진 점 근방에서 곡면의 국소적인 모양을 구체적으로 묘사할 수 있는 효율적인 테크닉은 있지만 곡면의 전체적인 모양을 기술하는 것은 아주 힘든 일이고 불가능해 보일 때도 있습니다.