Ulrich Pinkall, Nicholas Schmitt, Charles Gunn and Tim Hoffmann
미분기하는 곡선이나 곡면 또는 심지어 다차원의 모양 같이 굽어진 모양을 다루는 학문입니다. 미분기하의 관점으로 보았을 때, 비누막이나 비누방울들의 모양은 곡면의 모든 점에서 평균곡률이 같다는 점에서 특이합니다. 이 갤러리에서는 일정한 평균곡률을 갖는 면들을 보여줍니다. 한 사진은 최소면적을 갖지는 않지만 최소 곡면합을 갖는 면을 보여주고 다른 사진에서는 일정한 평균곡률을 갖는 삼차원 공간을 보여줍니다.
Discrete Minimal Surface
최소 곡면은 미분 기하학의 고전적인 주제 중 하나입니다. 이 곡면은 모든 곳에서 평균 곡률이 0인 곡면으로써, 현수면(Catenoid)과 나선면(Helicoid)이 가장 잘 알려진 극소 곡면입니다. 최소 곡면의 흥미로운 특징들 중 하나는 그성질을 유지한 채 변형될 수 있다는 점입니다.전문적으로 말하면, 한 모임에 속한 곡면들은 등거리이면서 대응하는 접평면이 평행하도록 변형될 수 있습니다. 현수면과 나선면은 한 모임에 속합니다. 결과적으로, 이 곡면들을 다른 곡면으로 변형할 수 있고, 변형 과정에서 나타나는 모든 곡면들도 최소 곡면들입니다.
이 그림은 현수면과 나선면의 변형 과정의 중간에 등장하는 최소 곡면을 이산화한 것 입니다. 이 곡면은 서로 접하는 구와 원으로 구성되어 있습니다. 또한, 이산화된 최소 곡면들 사이에도 서로 관련된 모임이 있는 데, 이 모임에 속하는 곡면들은 해당하는 구의 반지름과 원판의 위치가 모두 같습니다.
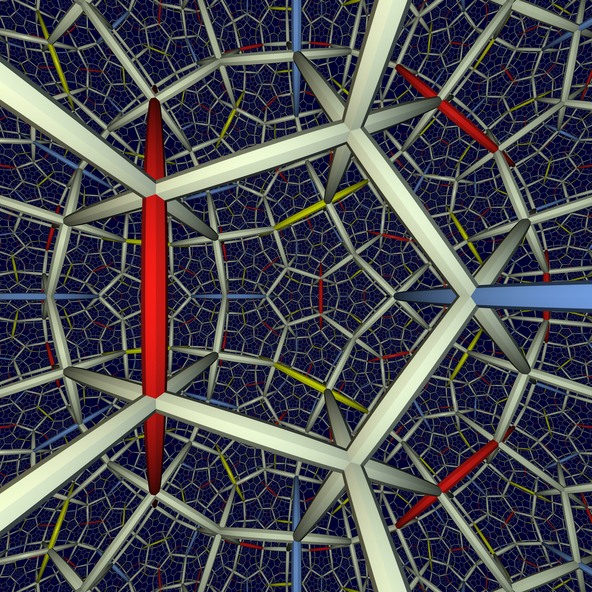
Hyperbolic Space
이 그림은 무수히 많은 정십이면체들로 채워진 3차원 쌍공공간을 보여줍니다. 쌍곡공간은 음의 곡률을 갖는 휘어진 공간입니다. 이 뜻은 거리들이 평평한 공간보다 빠르게 멀어진다는 것을 의미합니다.
그림에서 보이는 쌍곡공간에서 정십이면체들의 표면들은 서로 직교하고 있지만 이것은 평평한 기하에 익숙한 우리에게는 관찰하기 어렵습니다. 평평한 기하로 치면 이 상황은 공간이 정육면체들로 채워졌을 때 한 모서리 주위의 정육면체의 면들이 직교하는 것과 같습니다.
위에서와 같이 정십이면체들로 쌍곡공간을 채우는 것은 Borromean 고리들의 주변공간을 위상수학에서 기하학적으로 재현할 때 나타납니다. 그림에서 빨간색, 노란색, 파란색 선들은 꼬임을 유발시키는 세 개의 고리에 해당합니다. 이 그림은 쌍곡공간의 거주자에게 보이는 풍경을 보여줍니다. 쌍곡곡면에서의 빛과 광학을 도입하려는 시도도 있었습니다.
이 광경은 jReality로 개발되었고, 그림자체는 Renderman에 의해 계산되었습니다. 이 작업은 DFG Research Centre Matheon의 도움을 받았습니다.
Boy Surface
Boy 곡면은 원판의 가장자리에 뫼비우스 띠를 꿰매어 얻은 곡면을 매개화하여 얻을 수 있는 불가향 곡면(non-orientable) 곡면입니다. 1901년 Werner Boy가 발견한 이 곡면은 (자기 교차는 가지지만) 특이점이 없는 사영평면의 한 모델입니다.
Oberwolfach 수학연구소 입구 밖에는 메르세데스 - 벤츠가 만들어 기증한 큰 Boy 곡면이 설치되어 있습니다. 이 그림은 곡면의 평균 곡률이 가능한한 작도록 하여 얻었습니다. 이런 점에서 불필요한 돌출부가 없습니다. 지금 당신은 수학적으로 정확하면서도 가장 아름답게 구현된 Boy 곡면을 보고 있습니다. 이 그림은 Robert Bryant와 Robert Kusner가 Boy 곡면을 매개화한 것으로, Paul Debevec이 샌프란시스코의 한 교회의 사진으로 부터 만든 bullet panorama를 기반으로 합니다. 그림의 바탕은 jReality를 이용하여 컴파일되었고 그림 자체는 Sunflow를 이용하여 계산되었습니다.
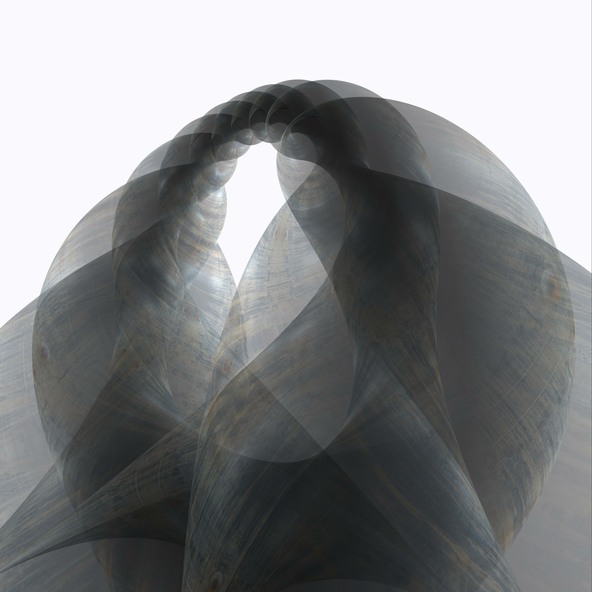
Helicoid with Handles
가장 잘 알려진 최소곡면 중 하나는, 나선형 계단, 혹은 주차 경사로 같은 모양인 Helicoid입다. 실제로 서로의 최소곡면성질을 파괴하지 않고 겹치는 부분 없이, 서로 다른 Helicoid의 시트를 연결할 수 있습니다.
이 연결 부분을 수학용어로 손잡이(handle)라 합니다. 당신이 몇층에 있는가에 따라서 이와 같은 손잡이는 바닥 혹은 천장에 난 구멍같이 보이기도 하고, 층이 바닥과 천장을 이어주는 기둥같이 보이기도 합니다.
이 곡면은 두개의 손잡이가 있는 Helicoid이고 Markus Schmies에 의해 발견 및 계산되었습니다. 배경은 Simon O’Callaghan에 의해 Terragen을 사용하여 컴퓨터로 생성된 경치를 기반으로 합니다. 그 장면은 jReality에서 컴파일 되었고, 이미지 그 자체는 Sunflow로 계산되었습니다. DFG-Research Centre Matheon에 의해 추진되었습니다.
Bursting Nodoid
Bursting Nodoid는 상수평균곡률을 갖는 특별한 곡면입니다. 비누방울이 특정한 기체공간을 둘러싸듯이, 그런 곡면은 다른 압력을 가지는 두 액체 혹은 기체 사이에 경계곡면으로서 상상 될 수 있습니다. 물리적인 비누방울과는 달리, 수학에서는 비누방울이 자기 스스로 교차하는 것을 허용합니다.
보이는 바와 같이 곡면으로부터 나오는 다섯 갈래의 부분 곡면들은 끝없이 연결될 것입니다. 네개의 물결치는 튜브가 위쪽 끝을 아래로 끌어당기고, 기둥이 위로 힘을 받는 가운데, 힘의 균형이 유지될 것입니다.
이 곡면은 Nicholas Schmitt(Geometrie-Werkstatt Tubingen)에 의해 개발되었습니다. 그는 XLab software를 이용한 이미지도 디자인하고 계산하였습니다.
Tetranoid
Tetranoid는 비누방울처럼 같은 곡률(curvature)을 갖는 곡면의 집단에 속합니다. 수학적으로는 Tetranoid는 “상수평균곡률”을 가지며, Tetranoid의 네 개의 다리는 실제로 끝나지 않습니다.
Tetranoid의 존재성(플라톤 입체들에 기반한 어떤 대칭성을 가지는 유사한 곡면의 존재성처럼)은 Nicholas Schmitt에 의해 증명되었습니다. 또한 그는 그 곡면을 계산했습니다.
그림은 Paul Bourke가 사진들로부터 생성한 총알 파노라마(bullet panorama)를 기반으로 합니다. 그 장면은 jReality 에서 컴파일 되었고, 이미지 그 자체는 Sunflow로 계산되었습니다. DFG-Research Centre Matheon에 의해 추진되었습니다.
Twizzle Torus
Twizzle Torus(나선형의 원환면)는 굽은 공간인 3차원 구에서 일정한 평균 곡률을 가지는 원환 형의 곡면입니다. 이를 육안으로 보기 위해서는 평면 공간으로 사영시켜야 합니다. 다행히 Twizzle Torus의 기본적인 특성을 유지하면서 사영시킬 수 있습니다. Twizzle Torus는 3차원 구에서 나선 대칭인데, 사영시키는 과정에서도 여전히 나선 대칭임을 예상할 수 있습니다. Twizzle Torus는 유사한 곡률의 성질을 가지면서 점점 복잡해지는 원환형 곡면들의 끝없는 계층(hierarchy) 중에서 유일하게 비교적 간단한 예입니다. 이 곡면은 Nicholas Schmit가 개발하였고, XLab software을 이용하여 설계하고 계산한 그림입니다.
Björling Surface
최소곡면은 비누막과 같은 곡률을 갖는 곡면입니다. 주어진 조건에 맞는 최소곡면을 만드는 것은 미분기하학의 매우 오래된 주제입니다. 1844년 E.G Björling 은 충분히 좋은 공간 곡선에 대하여 그 곡선을 포함하는 얇은 띠 모양의 최소곡면을 찾을 수 있다는 것을 보였습니다. 게다가 그 띠 모양의 곡면이 주어진 곡선 주위에서 얼마나 틀어져야 하는지 구체적으로 보였습니다.
위 그림은 나선곡선을 뼈대로 하여 일정한 속도로 휘어지는 띠 모양의 곡면입니다.
이 Björling 곡면의 방정식은 Matthias Weber 에 의해 만들어졌습니다. 그림의 배경은 Simon O’Callaghan에 의해 만들어진 Terragen 이라는 프로그램을 이용해 만들어진 인공적인 풍경입니다. 전체 그림은 jReality 라는 프로그램의 일부이고, 곡면은 Sunflow 라는 프로그램에 의해 계산되었습니다.