Random maps
program
Licenses
Source code
Website
Contributors
Random quadrangulation with 30 000 faces
Random quadrangulation with 50 000 faces
Random quadrangulation with 50 000 faces whose faces are randomly colored yellow or brown
Cactus embedding of a random quadrangulation with 50 000 faces
Random map with 50 000 edges (the faces are not necessarily quadrangles)
Random quadrangulation of the torus with 50 000 faces
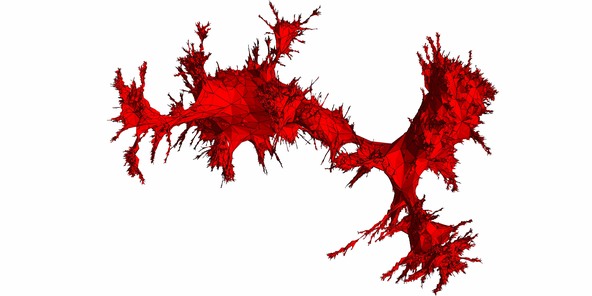
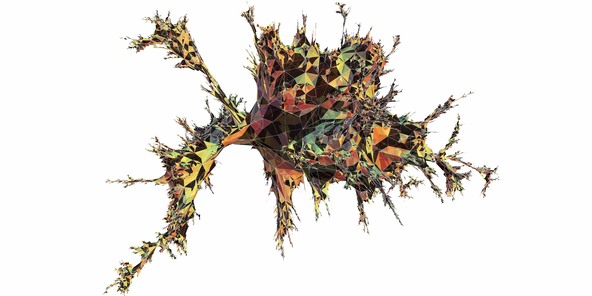
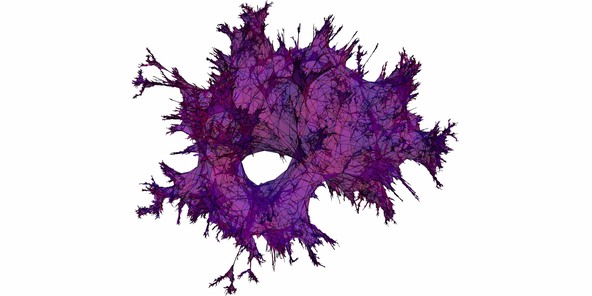
The following 3d model is a simulation of a uniform random quadrangulation with 30 000 faces. You can think of it as follows. If you are given 30 000 rubber squares, you can stitch them together along their sides and obtain a surface homeomorphic to the sphere. In plain English, this means that if you pump up the rubber surface, you obtain a sphere (think of a soccer ball for example). Put all the possible structures you can obtain by stitching together your squares in a bag and pick one at random.
You can visit my webpage for many more simulations and my picture page for many more higher quality downloadable pictures. In particular, you will find simulations of maps on more complicated surfaces (torus, double torus, disk, cylinder…).
To be more acurate, you can observe that each square face has been split into four subtriangles. This was done for a nicer looking embedding.
The map is embedded in 3d using a spring electrical embedding. It means that the computer tries to minimize an energy given by an electrical type of repulsion between vertices and a spring repeling force between vertices that are linked by an edge. The advantage of such an embedding is that the intrinsic metric on the surface reflects as best as possible the graph metric of the map.
