Ulrich Pinkall, Nicholas Schmitt, Charles Gunn ve Tim Hoffmann
galeri
Ulrich Pinkall, Nicholas Schmitt, Charles Gunn ve Tim Hoffmann
Diferansiyel geometri uzaydaki eğri çizgi ve yüzeyler gibi kavisli şekillerin ve hatta çok boyutlu şekillerin çalışıldığı bir alandır. Bir sabun katmanının ve baloncuğunun şekillerini düşünelim. Diferansiyel geometrinin bakış açısıyla, bu şekiller «ortalama eğrilik» (mean curvature) diye bilinen çokluğun bu yüzeylerin her noktasında aynı olması gerçeği sayesinde diğerlerinden ayrılır. Bu galeride «sabit ortalama eğriliğe» (constant mean curvature) sahip birçok görsel bulabilirsiniz. Örneğin bunlardan bir tanesi minimal alana sahip olmayıp minimal «toplam eğriliğe» sahip bir yüzeyi gösterirken, bir diğer görsel «sabit eğriliğe» (constant curvature) sahip üç boyutlu bir uzayı gösteriyor.
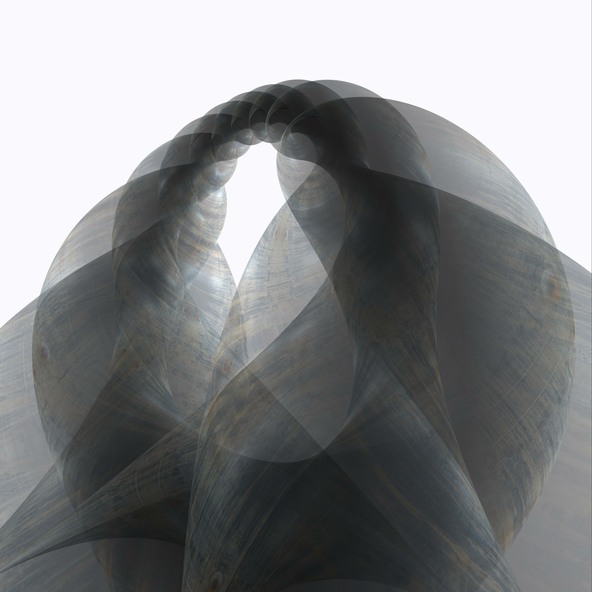
Ayrık Bir Minimal Yüzey
Minimal yüzeyler, türevli geometrinin klasik bir uğraş alanıdır. Minimal yüzeyler, ortalama eğriliği her yerde sıfır olan yüzeylerdir. Bu yüzey sınıfının en çok bilinenleri Katenoid ve Helikoid’dir. Minimal yüzeylerin bir çok ilginç özelliğinden biri, bunların bir aile olarak var olmasıdır. Bunun anlamı şudur: bir minimal yüzey, minimallik özelliğini kaybetmeden deforme edilebilir ve böylece aynı aileden birçok yüzey elde edilebilir. (Hatta aynı ailede olanlar birbirlerine izometriktirler ve karşılık gelen teğet düzlemleri birbirine paraleldir.) Helikoid ve Katenoid aynı aileye aittirler. Dolayısıyla bu iki yüzey birbirine dönüştürülebilir ve üstelik dönüşüm sırasındaki bütün yüzeyler de minimaldir.
Buradaki resim, Katenoid’den Helikoid’e deformasyonun tam orta anındaki minimal yüzeyi gösteriyor. Yüzey, birbirlerine teğet kürelerin ve çemberlerin birleştirilmesiyle oluşturulmuştur.
Lisans CC BY-NC-SA-3.0